如图,在矩形ABCD中,E是BC边上的点,AE=BC,DF⊥AE,垂足为F,连接DE.
(1)求证:△ABE≌△DFA;
(2)如果AD=10,AB=6,求sin∠EDF的值.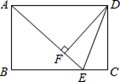
(·湖北荆门,22题,分)已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.
(1)求证:BD是⊙O的切线;
(2)求证: ;
;
(3)若⊙O的半径为5,sinA= ,求BH的长.
,求BH的长.
(·湖北黄冈,21题,分)已知:如图,在△ABC中,AB=AC,以AC为直径的⊙O 交AB 于点M,交BC 于点N,连接AN,过点C 的切线交AB 的延长线于点P.
(1)求证:∠BCP=∠BAN;
(2)求证: .
.
(·湖北鄂州,22题,9分)如图,在△ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线 BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交 AB于点F.
(1)求证:AE为⊙O的切线.
(2)当BC=8,AC=12时,求⊙O的半径.
(3)在(2)的条件下,求线段BG的长.
(·湖北衡阳,26题,分)(本小题满分8分)如图,AB是⊙O的直径,点C、D为半圆O的三等分点,过点C作CE⊥AD,交AD的延长线于点E.
(1)求证:CE为⊙O的切线;
(2)判断四边形AOCD是否为菱形?并说明理由.
(·湖南益阳)如图,在▱ABCD中,对角线AC与BD相交于点O,∠CAB=∠ACB,过点B作BE⊥AB交AC于点E.
(1)求证:AC⊥BD;
(2)若AB=14,cos∠CAB= ,求线段OE的长.
,求线段OE的长.