如图①在梯形ABCD中,AD∥BC。AB=DC
(1)如果点P,E和F分别是BC,AC和BD的中点,证明:AB=PE+PF
(2)如果点P是线段BC上任意一点(中点除外),PE∥AB,PF∥DC,如图②所示,那么AB=PE+PF这个结论还成立吗?请说明理由
(3)如果点P在线段BC的延长线上, PE∥AB,PF∥DC,其他条件不变,那么结论AB=PE+PF是否成立?直接写出结论,不必证明。
如图是重百商场的各个柜台分布平面示意图,请建立合适的直角坐标系,标出各个柜台的坐标. 
平行四边形ABCD,AD=6,AB=8,点A的坐标为(-3,0),求B、C、D各点的坐标。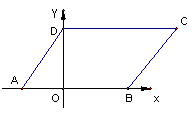
在直角坐标系中,四边形ABCD各个顶点的坐标分别为A(0,0),B(3,6),C(7,8),D(12,0),求四边形ABCD的面积.
如图,在下面的平面直角坐标系中,先画出以A(-2,3),B(-2,-3),C(-3.5,0)三点为顶点的三角形,再画出△ABC关于y轴对称的△ .
.
如图,是小王骑自行车离家的距离S(千米)与时间t (小时)之间的变化关系.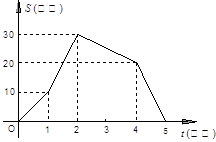
(1)根据图形填表:
| 时间t(小时) |
0 |
1 |
2 |
3 |
4 |
5 |
| 距离S(千米) |
(2)小王离家最远时是什么的时刻?这时离家有多远?
(3)他骑自行车最快的速度是多少?最慢的速度是多少?
(4)小王在哪一时刻与家相距20千米?