在平面直角坐标系xOy中,抛物线y= -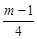 x2+
x2+ x+m2-3m+2 与x轴的交点分别为原点O和点A,点B(2,n)在这条抛物线上。
x+m2-3m+2 与x轴的交点分别为原点O和点A,点B(2,n)在这条抛物线上。

(1) 求点B的坐标;
(2) 点P在线段OA上,从O点出发向A点运动,过P点作x轴的垂线,与直线OB交于点E。延长PE到点D。使得ED=PE。 以PD为斜边在PD右侧作等腰直角三角形PCD(当P点运动时,C点、D点也随之运动)
j当等腰直角三角形PCD的顶点C落在此抛物线上时,求OP的长;
k若P点从O点出发向A点作匀速运动,速度为每秒1个单位,同时线段OA上另一点Q从A点出发向O点作匀速运动,速度为每秒2个单位(当Q点到达O点时停止运动,P点也同时停止运动)。过Q点作x轴的垂线,与直线AB交于点F。延长QF到点M,使得FM=QF,以QM为斜边,在QM的左侧作等腰直角三角形QMN(当Q点运动时,M点,N点也随之运动)。若P点运动到t秒时,两个等腰直角三角形分别有一条直角边恰好落在同一条直线上,求此刻t的值。
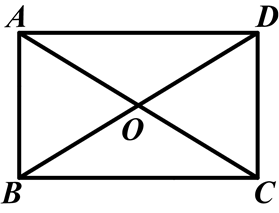
如图,矩形ABCD中,对角线AC,BD相交于点O,∠BOC=120°,AB=6.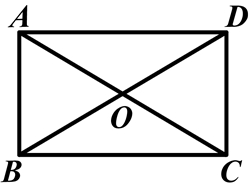
求:(1)对角线长;
(2)BC的长;
(3)矩形面积.
把长与宽之比为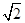 的矩形纸片称为标准纸,请思考并解决下列问题:
的矩形纸片称为标准纸,请思考并解决下列问题:
(1)将一张标准纸ABCD(AB<BC)对开,如图1所示,所得的矩形纸片ABEF是标准纸,请给予证明;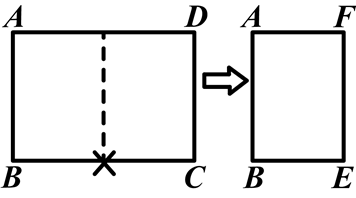
(2)在一次综合实践课上,小明尝试着将矩形纸片ABCD(AB<BC)进行如下操作:
第一步:沿过A点的直线折叠,使B点落在AD边上点F处,折痕为AE(如图2甲);
第二步:沿过D点的直线折叠,使C点落在AD边上点N处,折痕为DG(如图2乙),此时E点恰好落在AE边上的点M处;
第三步:沿直线DM折叠(如图2丙),此时点G恰好与N点重合.
请你探究:矩形纸片ABCD是否是一张标准纸,请说明理由;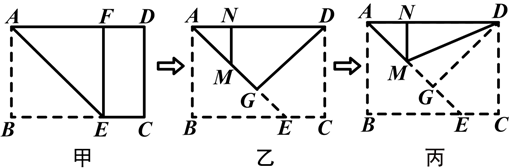
(3)不难发现:将一张标准纸按如图3所示方式一次又一次对开后,所得的矩形纸片都是标准纸,现有一张标准纸ABCD,AB=1,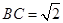 ,问第5次对开后所得标准纸的周长是多少?探索并直接写出第2014次对开后所得标准纸的周长.
,问第5次对开后所得标准纸的周长是多少?探索并直接写出第2014次对开后所得标准纸的周长.
如图,在四边形ABCD中,点H是边BC的中点,作射线AH,在线段AH及其延长线上分别取点E,F,连接BE,CF.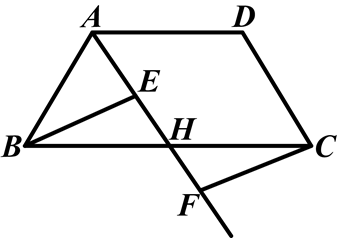
(1)请你添加一个条件,使得△BEH≌△CFH,你添加的条件是________,并证明;
(2)在问题(1)中,当BH与EH满足什么关系时,四边形BFCE是矩形?请说明理由.
如图,将□ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.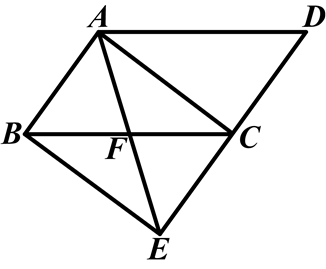
(1)求证:△ABF≌△ECF:
(2)若∠AFC=2∠D,连接AC、BE,求证:四边形ABEC是矩形.
如图,矩形ABCD的两条对角线相交于点O,∠AOD=120°,AB=6cm,求矩形的对角线长和面积.