要测量河两岸相对的两点A，B的距离，先在AB的垂线BF上取两点C，D，使CD=BC，再定出BF的垂线DE，使A，C，E在一条直线上（如图所示），可以说明△EDC≌△ABC，得ED=AB，因此测得ED的长就是AB的长，判定△EDC≌△ABC最恰当的理由是（ ）
| A．SAS | B．ASA | C．SSS | D．AAS |
对抛物线 而言，下列结论正确的是
| A． | 与x轴有两个交点 | B． | 开口向上 |
| C． | 与y轴交点坐标是 | D． | 顶点坐标是 |
如图（三）所示，已知O是直线AB上一点，∠1＝40°，OD平分∠BOC，则∠2的度数是
| A．20° | B．25° | C．30° | D．70° |
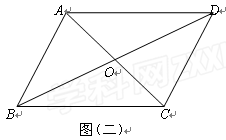
如图（二）所示，在□ABCD中，对角线AC、BD相交于点O，且AB≠AD，则下列式子不正确的是
| A．AC⊥BD | B．AB＝CD | C．BO＝OD | D．∠BAD＝∠BCD |
地球上水的总储量为1.39×1018m3，但目前能被人们生产、生活利用的水只占总储量的0.77％，即约为0.0107×1018m3，因此我们要节约用水．请将0.0107×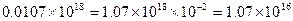
1018m3用科学记数法表示是
| A．1.07×1016m3 | B．0.107×1017m3 |
| C．10.7×1015m3 | D．1.07×1017m3 |
已知点(1，1)在反比例函数y＝(k为常数，k≠0)的图象上，则这个反比例函数的大致图象是