某机构为了研究人的脚的大小与身高之间的关系,随机测量了20人,得到如下数据
| 身高(厘米) |
192 |
164 |
172 |
177 |
176 |
159 |
171 |
166 |
182 |
166 |
| 脚长(码) |
48 |
38 |
40 |
43 |
44 |
37 |
40 |
39 |
46 |
39 |
| 身高(厘米) |
169 |
178 |
167 |
174 |
168 |
179 |
165 |
170 |
162 |
170 |
| 脚长(码) |
43 |
41 |
40 |
43 |
40 |
44 |
38 |
42 |
39 |
41 |
(1)若“身高大于175厘米”的为“高个”,“身高小于等于175厘米”的为“非高个”;“脚长大于42码”的为“大脚”,“脚长小于等于42码”的为“非大脚”,请根据上表数据完成下面的2×2列联表。
| |
高个 |
非高个 |
合计 |
| 大脚 |
|
|
|
| 非大脚 |
|
12 |
|
| 合计 |
|
|
20 |
(2)根据(1)中的2×2列联表,能有多少把握认为脚的大小与身高之间有关系。
某化工厂生产的某种化工产品,当年产量在150吨至250吨之间时,其生产的总成本 (万元)与年产量
(万元)与年产量 (吨)之间的函数关系式近似地表示为
(吨)之间的函数关系式近似地表示为 .问:(1)每吨平均出厂价为16万元,年产量为多少吨时,可获得最大利润?并求出最大利润;
.问:(1)每吨平均出厂价为16万元,年产量为多少吨时,可获得最大利润?并求出最大利润;
(2)年产量为多少吨时,每吨的平均成本最低? 并求出最低成本。
并求出最低成本。
已知

(1)当 时,求
时,求 ;
;
(2) 若
 ,求实数
,求实数 的取值范围.
的取值范围.
求值:

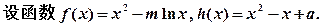
(1)当 时,
时,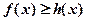 在
在 上恒成立,求实数
上恒成立,求实数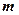 的取值范围;
的取值范围;
(2)当 时,若函数
时,若函数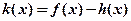 在
在 上恰有两个不同零点,求实数
上恰有两个不同零点,求实数 的取值范围;
的取值范围;
(3)是否存在实数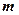 ,使函数f(x)和函数
,使函数f(x)和函数 在公共定义域上具有相同的单调区间?若存在,求出
在公共定义域上具有相同的单调区间?若存在,求出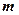 的值,若不存在,说明理由。
的值,若不存在,说明理由。
已知函数 (
(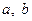 为实数,
为实数, ,
, ),
),
(1)若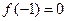 ,且函数
,且函数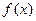 的值域为
的值域为 ,求
,求 的表达式;
的表达式;
(2)在(1)的条件下,当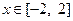 时,
时, 是单调函数,求实数
是单调函数,求实数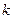 的取值范围;
的取值范围;
(3)设 ,
,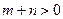 ,
, ,且函数
,且函数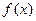 为偶函数,判断
为偶函数,判断 是否大于
是否大于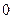 ?
?