已知某行星的半径为R,行星表面重力加速度为g,不考虑行星自转的影响。若有一卫星绕该行星做匀速圆周运动,运行轨道距行星表面高度为h,求卫星的运行周期T。
在边长为2a的正△ABC内存在垂直纸面向里的磁感强度为B的匀强磁场,有一带正电q,质量为m的粒子从距A点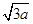 的D点垂直AB方向进入磁场,如下图所示,求:
的D点垂直AB方向进入磁场,如下图所示,求: 
(1)粒子速率应满足什么条件,粒子能从AB间射出;
(2)粒子速率应满足什么条件,粒子能从AC间射出。
某塑料球成型机工作时.可以喷出速度v0=10m/s的塑料小球,已知喷出的每个小球的质量m=1.0×10-4kg,并且在喷出时已带了q= -1.0×10-4C的电荷量。如图所示,小球从喷口飞出后,先滑过长为d=1.5m的水平光滑的绝缘轨道,而后又滑过半径为R=0.4m的圆弧形竖立的光滑绝缘轨道并从某处飞出。今在水平轨道上加上水平向右的场强大小为E的匀强电场,小球将恰好从圆弧轨道的最高点M处水平飞出;若再在圆形轨道区域加上垂直纸面向里的匀强磁场后,小球将恰好滑过圆弧轨道上与圆心等高的N点,最后落入放在地面上接地良好的金属容器内,g取10m/s2,求: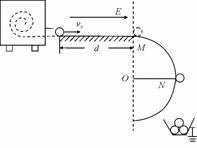
(1)所加电场的场强E多大?
(2)所加磁感应强度B多大?在此种情况下,小球经过M点时对轨道的压力多大?
下图所示为对光电效应产生的光电子进行比荷(电荷量e与质量 m 之比)测定的简要原理图,两块平行金属板M.N相距为d,其中N为锌板,受某一紫外光照射后将激发沿不同方向运动的光电子,开关S闭合后电流表G有读数.如果调节变阻器R ,逐渐增大极板间电压,电流表G的读数将逐渐减小,当电压表的读数为U时,电流表G的读数恰为零.如果断开开关S,在金属板M.N间加上垂直纸面的匀强磁场,当磁感应强度为B时,电流表G的读数也恰为零.求光电子的比荷e/m 的表达式.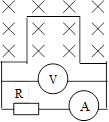
如图所示,半径为R的绝缘圆筒中有沿轴线方向的匀强磁场,磁场方向垂直于纸面向里,匀强磁场的磁感应强度为B,圆筒形场区的边界由弹性材料构成。一个质量为m.电荷量为q的正离子(不计重力)以某一速度从筒壁上的小孔M进入筒中,速度方向与半径成θ=30°夹角,并垂直于磁场方向。离子和筒壁的碰撞无能量和电荷量的损失.若选择合适的进入速度,离子可以从M孔射出。问: 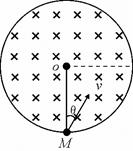
(1)离子的速度多大时,离子可以在最短的时间内返回M孔最短的时间是多少?
(2)如果离子与筒壁发生两次碰撞后从M孔射出,离子的速率是多大?从进入圆筒到返回M孔经历的时间是多少?
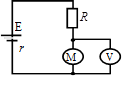
如图所示,电源的电动势为50V,电源内阻为1.0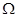 ,定值电阻R=14
,定值电阻R=14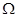 ,M为直流电动机,电枢电阻R′=2.0
,M为直流电动机,电枢电阻R′=2.0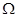 ,电动机正常运转时,电压表读数为35V,求在100s时间内电源做的功和电动机上转化为机械能的部分是多少?
,电动机正常运转时,电压表读数为35V,求在100s时间内电源做的功和电动机上转化为机械能的部分是多少?