均匀导线制成的单匝正方形闭合线框abcd,每边长为L,总电阻为R,总质量为m.将其置于磁感强度为B的水平匀强磁场上方h处,如图20所示.线框由静止自由下落,线框平面保持在竖直平面内,且cd边始终与水平的磁场边界面平行.当cd边刚进入磁场时:
(1)求线框中产生的感应电动势大小.
(2)求cd两点间的电势差大小.
(3)若此时线框加速度恰好为零,求线框下落的高度h所应满足的条件.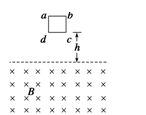
右图电路中R1=12 Ω,R2=6 Ω,滑动变阻器R3上标有“20 Ω,2 A”字样,理想电压表的量程有0~3 V和0~15 V两挡,理想电流表的量程有0~0.6 A和0~3 A两挡.闭合开关S,将滑片P从最左端向右移动到某位置时,电压表、电流表示数分别为2.5 V和0.3 A;继续向右移动滑片P至另一位置,电压表指针指在满偏的1/3,电流表指针指在满偏的1/4,求: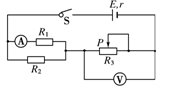
(1)此时电流表示数;
(2)电源的电动势.
一台小型电动机在3 V电压下工作,用此电动机提升所受重力为4 N的物体时,通过它的电流是0.2 A.在30 s内可使该物体被匀速提升3 m.若不计除电动机线圈生热之外的能量损失,求:
(1)电动机的输入功率;
(2)在提升重物的30 s内,电动机线圈所产生的热量;
(3)线圈的电阻.
如图所示的电路中,E=10 V,R1=4 Ω,R2=6 Ω,电池内阻不计,C1=C2=30 μF.先闭合开关S,待电路稳定后再断开S,求断开S后通过电阻R1的电荷量.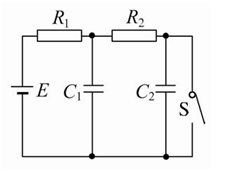
(14分)如图所示,电阻R1="2" Ω,小灯泡L上标有“3 V,1.5 W”,电源内阻r="1" Ω,滑动变阻器的最大阻值为R0(大小未知),当触头P滑动到最上端a时,电流表的读数为1 A,小灯泡L恰好正常发光,求:
(1)滑动变阻器的最大阻值R0.
(2)当触头P滑动到最下端b时,求电源的总功率及输出功率.
来自质子源的质子(初速度为零),经一加速电压为800 kV的直线加速器加速,形成电流为1 mA的细柱形质子流.
(1)已知质子电荷量e=1.60×10-19 C,这束质子流每秒打到靶上的质子数为多少?
(2)假定分布在质子源到靶之间的加速电场是均匀的,在质子束中与质子源相距l和4l的两处,各取一段极短的相等长度的质子流,其中的质子数分别为n1和n2,求n1∶n2.