问题情境:将一副直角三角板(Rt△ABC和Rt△DEF)按图1所示的方式摆放,其中∠ACB=90°,CA=CB,∠FDE=90°,O是AB的中点,点D与点O重合,DF⊥AC于点M,DE⊥BC于点N,试判断线段OM与ON的数量关系,并说明理由.
探究展示:小宇同学展示出如下正确的解法:
解:OM=ON,证明如下:
连接CO,则CO是AB边上中线,
∵CA=CB,∴CO是∠ACB的角平分线.(依据1)
∵OM⊥AC,ON⊥BC,∴OM=ON.(依据2)
反思交流:
(1)上述证明过程中的“依据1”和“依据2”分别是指:
依据1:
依据2:
(2)你有与小宇不同的思考方法吗?请写出你的证明过程.
拓展延伸:
(3)将图1中的Rt△DEF沿着射线BA的方向平移至如图2所示的位置,使点D落在BA的延长线上,FD的延长线与CA的延长线垂直相交于点M,BC的延长线与DE垂直相交于点N,连接OM、ON,试判断线段OM、ON的数量关系与位置关系,并写出证明过程.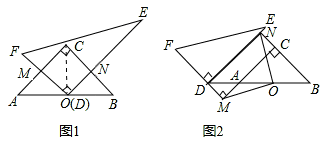
计算: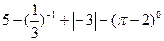
对非负实数x“四舍五入”到个位的值记为
即:当n为非负整数时,如果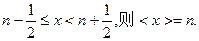
如:<0>=<0.48>=0,<0.64>=<1.493>=1,<2>=2,<3.5>=<4.12>=4,…
试解决下列问题:
(1)填空:① =(
=(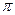 为圆周率);
为圆周率);
②如果 的取值范围为;
的取值范围为;
(2)①当 ;
;
②举例说明 不恒成立;
不恒成立;
(3)求满足 的值;
的值;
(4)设n为常数,且为正整数,函数 范围内取值时,函数值y为整数的个数记为
范围内取值时,函数值y为整数的个数记为 的个数记为b.
的个数记为b.
求证: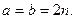
如图,在直角坐标系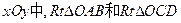 的直角顶点A,C始终在x轴的正半轴上,B,D在第一象限内,点B在直线OD上方,OC=CD,OD=2,M为OD的中点,AB与OD相交于E,当点B位置变化时,
的直角顶点A,C始终在x轴的正半轴上,B,D在第一象限内,点B在直线OD上方,OC=CD,OD=2,M为OD的中点,AB与OD相交于E,当点B位置变化时,
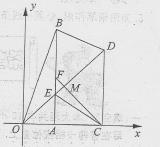
试解决下列问题:
(1)填空:点D坐标为;
(2)设点B横坐标为t,请把BD长表示成关于t的函数关系式,并化简;
(3)等式BO=BD能否成立?为什么?
(4)设CM与AB相交于F,当△BDE为直角三角形时,判断四边形BDCF的形状,并证明你的结论.
如图,已知△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过D作DE⊥BC,垂足为E,连结OE,CD= ,∠ACB=30°.
,∠ACB=30°.
(1)求证:DE是⊙O的切线;
(2)分别求AB,OE的长;
(3)填空:如果以点E为圆心,r为半径的圆上总存在不同的两点到点O的距离为1,则r的取值范围为.
海宝在研究数学问题时发现了一个有趣的现象:
(1)请你用数学表达式补充完整海宝发现的这个有趣的现象;
(2)请你证明海宝发现的这个有趣现象.