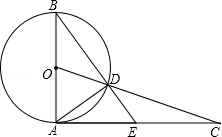
周末,小明骑自行车从家里出发到野外郊游.从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地.小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.已知妈妈驾车的速度是小明骑车速度的3倍.
(1)求小明骑车的速度和在甲地游玩的时间;
(2)小明从家出发多少小时后被妈妈追上?此时离家多远?
(3)若妈妈比小明早10分钟到达乙地,求从家到乙地的路程.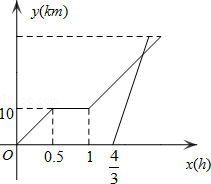
已知反比例函数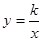 的图象经过点M(2,1).
的图象经过点M(2,1).
(1)求该函数的表达式;
(2)当 时,求
时,求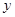 的取值范围.(直接写出结果)
的取值范围.(直接写出结果)
如图,已知抛物线y=ax2+bx+c与x轴的一个交点为A(3,0),与y轴的交点为B(0,3),其顶点为C,对称轴为x=1.
(1)求抛物线的解析式;
(2)已知点M为y轴上的一个动点,当△ABM为等腰三角形时,求点M的坐标;
(3)将△AOB沿x轴向右平移m个单位长度(0<m<3)得到另一个三角形,将所得的三角形与△ABC重叠部分的面积记为S,用m的代数式表示S.
如图,已知直线l1∥l2,线段AB在直线l1上,BC垂直于l1交l2于点C,且AB=BC,P是线段BC上异于两端点的一点,过点P的直线分别交l2、l1于点D、E(点A、E位于点B的两侧),满足BP=BE,连接AP、CE.
(1)求证:△ABP≌△CBE;
(2)连结AD、BD,BD与AP相交于点F.如图2.
①当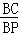 =2时,求证:AP⊥BD;
=2时,求证:AP⊥BD;
②当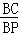 =n(n>1)时,设△PAD的面积为S1,△PCE的面积为S2,求
=n(n>1)时,设△PAD的面积为S1,△PCE的面积为S2,求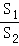 的值.
的值.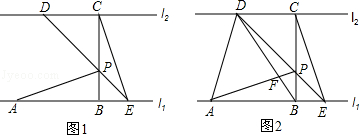
某商家计划从厂家采购空调和冰箱两种产品共20台,空调的采购单价y1(元/台)与采购数量x1(台)满足y1=﹣20x1+1500(0<x1≤20,x1为整数);冰箱的采购单价y2(元/台)与采购数量x2(台)满足y2=﹣10x2+1300(0<x2≤20,x2为整数).
(1)经商家与厂家协商,采购空调的数量不少于冰箱数量的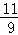 ,且空调采购单价不低于1200元,问该商家共有几种进货方案?
,且空调采购单价不低于1200元,问该商家共有几种进货方案?
(2)该商家分别以1760元/台和1700元/台的销售单价售出空调和冰箱,且全部售完.在(1)的条件下,问采购空调多少台时总利润最大?并求最大利润.
如图,AB是⊙O的直径,过点A作⊙O的切线并在其上取一点C,连接OC交⊙O于点D,BD的延长线交AC于E,连接AD.
(1)求证:△CDE∽△CAD;
(2)若AB=2,AC=2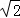 ,求AE的长.
,求AE的长.