小刚平面直角坐标系中画了一张脸,他对妹妹说;“如果我用(1,3)表示左眼,用(3,3)表示右眼,那么嘴的位置可以表示成( )
| A.(1,2) | B.(2,3) | C.(3,2) | D.(2,1) |
已知b<0时,二次函数 的图象如下列四个图之一所示.根据图象分析,a的值等于
的图象如下列四个图之一所示.根据图象分析,a的值等于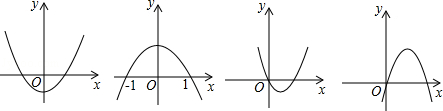
| A.-2 | B.-1 | C.1 | D.2 |
如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1,S2,则S1+S2的值为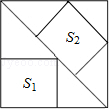
| A.16 | B.17 | C.18 | D.19 |
一条直线y=kx+b,其中k+b=﹣5、kb=6,那么该直线经过
| A.第二、四象限 | B.第一、二、三象限 | C.第一、三象限 | D.第二、三、四象限 |
如图,数轴上的A、B、C三点所表示的数分别是a、b、c,其中AB=BC,如果|a|>|b|>|c|,那么该数轴的原点O的位置应该在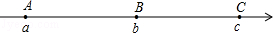
A.点A的左边 B.点A与点B之间
C.点B与点C之间 D.点B与点C之间或点C的右边
在我市举行的中学生春季田径运动会上,参加男子跳高的15名运动员的成绩如下表所示:
这些运动员跳高成绩的中位数和众数分别是
| A.1.70,1.65 | B.1.70,1.70 | C.1.65,1.70 | D.3,4 |