如图1,在直角坐标系 中,抛物线
中,抛物线 :
: 与
与 轴交于点
轴交于点 ,以
,以 为一边向左侧作正方形
为一边向左侧作正方形 上;如图2,把正方形
上;如图2,把正方形 绕点
绕点 顺时针旋转
顺时针旋转 后得到正方形
后得到正方形 (
( ﹤
﹤ ﹤
﹤ )﹒
)﹒

(1) 、
、 两点的坐标分别为 、 ;
两点的坐标分别为 、 ;
(2)当 tan ﹦
﹦ 时,抛物线
时,抛物线 的对称轴上是否存在一点
的对称轴上是否存在一点 ,使△
,使△ 为直角三角形?若存在,请求出所有点
为直角三角形?若存在,请求出所有点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(3)在抛物线 的对称轴上是否存在一点
的对称轴上是否存在一点 ,使△
,使△ 为等腰直角三角形?若存在,请直接写出此时tan
为等腰直角三角形?若存在,请直接写出此时tan 的值;若不存在,请说明理由﹒
的值;若不存在,请说明理由﹒
四张小卡片上分别写有数字1、2、3、4.它们除数字外没有任何区别,现将它们放在盒子里搅匀.
(1)随机地从盒子里抽取一张,求抽到数字2的概率;
(2)随机地从盒子里抽取一张.不放回再抽取第二张.请你用画树状图或列表的方法表示所有等可能的结果,并求抽到的数字之和为5的概率.
小明、小亮利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时间,身高为 的小明
的小明 的影子
的影子 长是
长是 ,而小亮
,而小亮 刚好在路灯灯泡的正下方
刚好在路灯灯泡的正下方 点,并测得
点,并测得 .
.
(1)请在图中画出形成影子的光线,交确定路灯灯泡所在的位置 ;
;
(2)求路灯灯泡的垂直高度 .
.
如图,一条河的两岸有一段是平行的,在河的南岸边每隔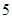 米有一棵树,在北岸边每隔
米有一棵树,在北岸边每隔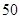 米有一根电线杆.小丽站在离南岸边
米有一根电线杆.小丽站在离南岸边 米的点
米的点 处看北岸,发现北岸相邻的两根电线杆A、B,恰好被南岸的两棵树C、D遮住,并且在这两棵树之间还有三棵树,求河的宽度.
处看北岸,发现北岸相邻的两根电线杆A、B,恰好被南岸的两棵树C、D遮住,并且在这两棵树之间还有三棵树,求河的宽度.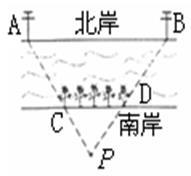
(1)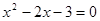
(2)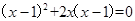
如图,一艘海轮位于灯塔P的南偏东45°方向,距离灯塔100海里的A处,它计划沿正北方向航行,去往位于灯塔P的北偏东30°方向上的B处.
(1)B处距离灯塔P有多远?
(2)圆形暗礁区域的圆心位于PB的延长线上,距离灯塔200海里的O处.已知圆形暗礁区域的半径为50海里,进入圆形暗礁区域就有触礁的危险.请判断若海轮到达B处是否有触礁的危险,并说明理由.