如图，把两个全等的Rt△AOB和Rt△COD分别置于平面直角坐标系中，使直角边OB、OD在x轴上．已知点A（1，2），过A、C两点的直线分别交x轴、y轴于点E、F．抛物线y=ax²+bx+c经过O、A、C三点．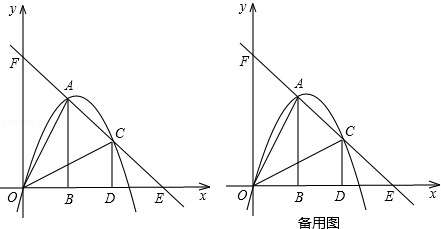

（1）求该抛物线的函数解析式；
（2）点P为线段OC上一个动点，过点P作y轴的平行线交抛物线于点M，交x轴于点N，问是否存在这样的点P，使得四边形ABPM为等腰梯形？若存在，求出此时点P的坐标；若不存在，请说明理由．
（3）若△AOB沿AC方向平移（点A始终在线段AC上，且不与点C重合），△AOB在平移过程中与△COD重叠部分面积记为S．试探究S是否存在最大值？若存在，求出这个最大值；若不存在，请说明理由．

科目 数学   题型 解答题   难度 较难

知识点： 二次函数在给定区间上的最值