小明和同桌小聪在课后复习时,对课本“目标与评定”中的一道思考题,进行了认真的探索。
【思考题】如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时B到墙C的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么点B将向外移动多少米?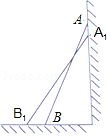
(1)请你将小明对“思考题”的解答补充完整:
解:设点B将向外移动x米,即BB1=x,
则B1C=x+0.7,A1C=AC﹣AA1=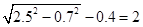
而A1B1=2.5,在Rt△A1B1C中,由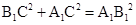 得方程 ,
得方程 ,
解方程得x1= ,x2= ,
∴点B将向外移动 米。
(2)解完“思考题”后,小聪提出了如下两个问题:
【问题一】在“思考题”中,将“下滑0.4米”改为“下滑0.9米”,那么该题的答案会是0.9米吗?为什么?
【问题二】在“思考题”中,梯子的顶端从A处沿墙AC下滑的距离与点B向外移动的距离,有可能相等吗?为什么?
请你解答小聪提出的这两个问题。
如图所示,甲船在港口P的北偏西600的方向且距港口80海里的A处,沿AP方向以12海里/时的速度驶向港口P.乙船从港口P出发,沿北偏东450方向匀速驶离港口P,现两船同时出发,2小时后乙船恰在甲船的正东方向.求乙船的航行速度.(精确到0.1海里/时,参考数据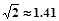 ,
, )
)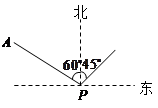
已知:如 图,△
图,△ 和△
和△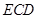 都是等
都是等 腰直角三角形,
腰直角三角形, ,
,
点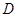 在
在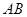 上.求证:
上.求证: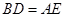
现有一张长和宽之比为2:1的长方形纸片.将它折两次(第一次折后也可以打开铺平再折第二次).使得折痕将纸片分为面积相等且不重叠的四个部分(称为一个操作),如图甲(虚线表示折痕).
除图甲外,请你再给出三个不同的操作,分别将折痕画在图①至图③中(规定:一个操作得到的四个图形,和另一个操作得到的四个图形,如果能够“配对”得到四组全等的图形,那么就认为是相同的操作.如图乙和图甲是相同的操作).
图①图②图③
高致病性禽流感是比SARS病毒传染速度更快的传染病。
某养殖场有8万只鸡,假设有1只鸡得了禽流感,如果不采取任何防治措施,那么,到第二天将新增病鸡10只,到第三天又将新增病鸡100只,以后每天新增病鸡数依次类推,请问:到第四天,共有多少只鸡得了禽流感病?到第几天,该养殖场所有鸡都会被感染?
为防止禽流感蔓延,政府规定:离疫点3千米范围内为扑杀区,所有禽类全部扑杀;离疫点3至5千米范围内为免疫区,所有的禽类强制免疫;同时,对扑杀区和免疫区内的村庄.道路实行全封闭管理。现有一条笔直的公路AB通过禽流感病区,如图11,O为疫点,在扑杀区内的公路CD长为4千米,问这条公路在该免疫区风有多少千米?
某商场今年2月份的营业额为400万元,3月份的营业额比2月份增加10%,5月份的营业额达到633.6万元.求3月份到5月份营业额的月平均增长率.