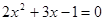为贯彻落实省教育厅提出的“三生教育”.在母亲节来临之际,某校团委组织了以“珍爱生命,
学会生存,感恩父母”为主题的教育活动,在学校随机调查了50名同学平均每周在家做家务的时间,统
计并制作了如下的频数分布表和扇形统计图:
| 组别 |
做家务的时间 |
频数 |
频率 |
| A |
1≤t<2 |
3 |
0.06 |
| B |
2≤t<4 |
20 |
0.40 |
| C |
4≤t<6 |
a |
0.30 |
| D |
6≤t<8 |
8 |
b |
| E |
t≥8 |
4 |
0.08 |
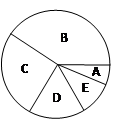
根据上述信息回答下列问题:
(1)a= ,b= .
(2)在扇形统计图中,B组所占圆心角的度数为 .
(3)全校共有2000名学生,估计该校平均每周做家务时间不少于4小时的学生约有多少人?
阅读下面的材料,并解答问题:
材料:已知当a、b是正数时,有下列命题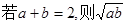 ≤1
≤1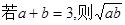 ≤
≤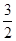
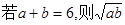 ≤ 3
≤ 3
(1)根据以上三个命题所提供的规律猜想: ≤ ;
≤ ;
(2)以上规律可用字母表示为 ;
(3)建造一个容积为8立方米,深2米的长方形无盖水池,池底和池壁的造价分别为每平方米120元和80元.设池底的长为x米,水池总造价为y元,应用上述的规律,求水池的最低造价.
为了比较市场上甲、乙两种电子钟每日走时误差的情况,从这两种电子钟中,各随机抽取10台进行测试,两种电子钟走时误差的数据如下表(单位:秒):
| 编号 类型 |
一 |
二 |
三 |
四 |
五 |
六 |
七 |
八 |
九 |
十 |
| 甲种电子钟 |
1 |
-3 |
-4 |
4 |
2 |
-2 |
2 |
-1 |
-1 |
2 |
| 乙种电子钟 |
4 |
-3 |
-1 |
2 |
-2 |
1 |
-2 |
2 |
-2 |
1 |
(1) 计算甲、乙两种电子钟走时误差的平均数;
(2) 计算甲、乙两种电子钟走时误差的方差;
(3) 根据经验,走时稳定性较好的电子钟质量更优.若两种类型的电子钟价格相同,请问:你买哪种电子钟?为什么?
已知:如图,△ABC中,AD是BC边上的中线,四边形ABDE是平行四边形
(1)求证:四边形ADCE是平行四边形;
(2)当△ABC满足什么条件时,四边形ADCE是菱形?说明你的理由.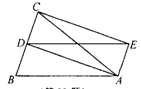
解方程: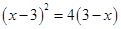
解方程: