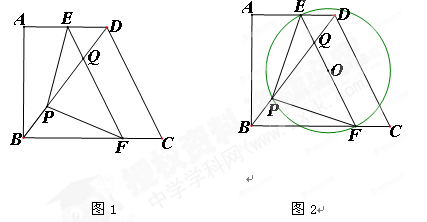
如图1，在直角梯形ABCD中，AD//BC，∠A=90°，AB=8cm，AD=6cm， BC=10cm。点P从点B出发沿BD方向匀速运动，速度为1cm/s；同时，线段EF从CD出发沿DA方向匀速运动，速度为1 cm/s，且EF与BD交于点Q，连接PE、PF。当点P与点Q相遇时，所有运动停止。若设运动时间为t（s）.
(1)求CD的长度
(2)当PE//AB时，求t的值；
(3)①设△PEF的面积为S，求S关于t的函数关系式；
②如图2，当△PEF的外接圆圆心O恰好在EF中点时，则t的值为 （请直接写出答案）
中，
，求证
，
，
，
四个顶点共圆．
的对角线
和
相交于
点，
，
，
，
分别是
，
，
，
的中点，求证：
，
是
的两条直径．求证：四边形
为矩形．
，投2分球命中的平均概率为
，问选择哪一种投篮方式，甲队取胜的可能性大一点？