以下是某省2010年教育发展情况有关数据:
全省共有各级各类学校25000所,其中小学12500所,初中2000所,高中450所,其它学校10050所;全省共有在校学生995万人,其中小学440万人,初中200万人,高中75万人,其它280万人;全省共有在职教师48万人,其中小学20万人,初中12万人,高中5万人,其它11万人.
请将上述资料中的数据按下列步骤进行统计分析.
(1)整理数据:请设计一个统计表,将以上数据填入表格中.
(2)描述数据:下图是描述全省各级各类学校所数的扇形统计图,请将它补充完整.
(3)分析数据:
①分析统计表中的相关数据,小学、初中、高中三个学段的师生比,最小的是哪个学段?请直接写出.(师生比=在职教师数︰在校学生数)
②根据统计表中的相关数据,你还能从其它角度分析得出什么结论吗?(写出一个即可)
③从扇形统计图中,你得出什么结论?(写出一个即可)

已知直线l为x+y=8,点P(x,y)在l上,且x>0,y>0,点A的坐标为(6,0).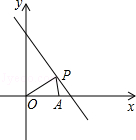
(1)设△OPA的面积为S,求S与x的函数关系式,并直接写出x的取值范围;
(2)当S=9时,求点P的坐标;
(3)在直线l上有一点M,使OM+MA的和最小,求点M的坐标.
某商场欲购进果汁饮料和碳酸饮料共50箱,两种饮料每箱的进价和售价如下表所示.设购进果汁饮料x箱(x为正整数),且所购进的两种饮料能全部卖出,获得的总利润为W元(注:总利润=总售价﹣总进价).
(1)设商场购进碳酸饮料y箱,直接写出y与x的函数关系式;
(2)求总利润w关于x的函数关系式;
(3)如果购进两种饮料的总费用不超过2100元,那么该商场如何进货才能获利最多?并求出最大利润.
饮料 果汁饮料 碳酸饮料
进价(元/箱) 51 36
售价(元/箱) 61 43
已知▱ABCD中,AE平分∠BAD,CF平分∠BCD,分别交CD、AB于E、F,求证:AE=CF.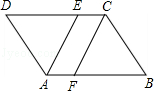
某人欲横渡一条河,由于水流的影响,实际上岸地点C偏离了欲到达点B,结果离欲到达点B 240米,已知他在水中游了510米,求该河的宽度(两岸可近似看做平行).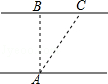
如图,已知,在平面直角坐标系中,A(﹣3,﹣4),B(0,﹣2).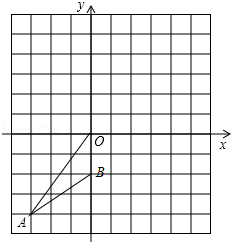
(1)△OAB绕O点旋转180°得到△OA1B1,请画出△OA1B1,并写出A1,B1的坐标;
(2)判断以A,B,A1,B1为顶点的四边形的形状,并说明理由.