九年级上册的教材第118页有这样一道习题:
“在一块三角形余料ABC中,它的边BC=120mm,高线AD=80mm.要把它加工成正方形零件(如图),使正方形的一边在BC上,其余两个顶点分别在AB,AC上.问加工成的正方形零件的边长为多少mm?”
(1)请你解答上题;
(2)若将上题图中的正方形PQMN改为矩形,其余条件不变,求矩形PQMN的面积S的最大值;
(3)我们把上面习题中的正方形PQMN叫做“BC边上的△ABC的内接正方形”,若在习题的条件下,又知AB=150mm,AC=100mm,请分别写出AB边上的△ABC的内接正方形的边长和AC边上的△ABC的内接正方形的边长(不必写出过程,只要直接写出答案即可,结果精确到1mm);
(4)结合第(1)、(3)题,若三角形的三边长分别为a,b,c,各边上的高分别为ha,hb,hc,要使a边上的三角形内接正方形的面积最大,请写出a与ha必须满足的条件(不必写出过程). 
如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.

(1)求线段CD的长;
(2)设△CPQ的面积为S,求S与t之间的函数关系式,并确定在运动过程中是否存在某一时刻t,使得S△CPQ:S△ABC=9:100?若存在,求出t的值;若不存在,则说明理由.
(3)是否存在某一时刻t,使得△CPQ为等腰三角形?若存在,求出所有满足条件的t的值;若不存在,则说明理由.
如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.
(1)求证:AC平分∠DAB;
(2)求证:PC=PF;
(3)若tan∠ABC= ,AB=14,求线段PC的长.
,AB=14,求线段PC的长.
如图,二次函数的图象与x轴交于A(﹣3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
(1)求二次函数的解析式;
(2)根据图象直接写出使一次函数值大于二次函数值的x的取值范围;
(3)若直线与y轴的交点为E,连结AD、AE,求△ADE的面积.
为了解中考体育科目训练情况,某县从全县九年级学生中随机抽取了部分学生进行了一次中考体育科目测试(把测试结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格),并将测试结果绘成了如下两幅不完整的统计图.请根据统计图中的信息解答下列问题: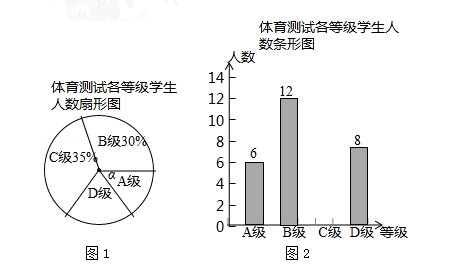
(1)本次抽样测试的学生人数是,其中不及格人数占样本人数的百分比为;
(2)图1中∠α的度数是,并把图2条形统计图补充完整;
(3)测试老师想从4位同学(分别记为E、F、G、H,其中E为小明)中随机选择两位同学了解平时训练情况,请用列表或画树形图的方法求出选中小明的概率.
从广州某市,可乘坐普通列车或高铁,已知高铁的行驶路程是400千米,普通列车的行驶路程是高铁的行驶路程的1.3倍.
(1)求普通列车的行驶路程;
(2)若高铁的平均速度(千米/时)是普通列车平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求高铁的平均速度.