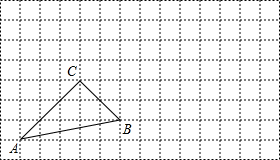
△ABC是一块等边三角形的废铁片，利用其剪裁一个正方形DEFG，使正方形的一条边DE落在BC上，顶点F、G分别落在AC、AB上．
(1) 证明：△BDG≌△CEF；
(2) 设△ABC的边长为2，请你帮小聪求出正方形的边长．（结果精确到十分位）
(3) 小颖想：不求正方形的边长我也能画出正方形．具体作法是：如图3
①在AB边上任取一点G′，如图作正方形G′D′E′F′；
②连接BF′并延长交AC于F；
③作FE∥F′E′交BC于E，FG∥F′G′交AB于G，GD∥G′D′交BC于D，则四边形DEFG即为所求．你认为小颖的作法正确吗？请说明理由．
和谐商场销售甲，乙两种商品，甲钟商品每件进价15元，售价20元；乙种商品每件进价35元，售价45元。
（1）若该商场同时购进甲，乙两种商品共100件，恰好用去2700元，求能购进甲，乙两种商品各多少件？
（2）该商场为使甲，乙两种商品共100件的总利润（利润=售价—进价）不少于750元，且不超过760元，请你帮助该商场设计相应的进货方案。
已知关于x，y的方程组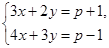
的解满足x＞y，求p的取值范围．
已知：如图，△ABC和△CDE都是等边三角形，点D在BC边上．求证：AD=BE．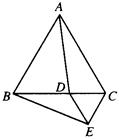 
已知：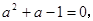
(1)求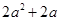
的值；
(2)求
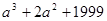的值。
作图题：
（1）把△ABC向右平移5个方格;
（2）绕点B的对应点顺时针方向旋转90°．