如图所示在三角形△ABC中AB=AC,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别为E、F,则下列四个结论中,①AB上一点与AC上一点到D的距离相等;②AD上任意一点到AB、AC的距离相等;③∠BDE=∠CDF;④BD=CD,AD⊥BC。其中正确的个数是
A.1个 B.2个 C.3个 D.4个
一件工程甲单独做a小时完成,乙单独做b小时完成,甲、乙二人合作完成此项工作需要的小时数是 ( )
| A.a+b | B.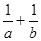 |
C.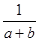 |
D.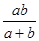 |
关于x的方程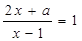 的解是正数,则a的取值范围是
的解是正数,则a的取值范围是
| A.a>-1 | B.a>-1且a≠0 |
| C.a<-1 | D.a<-1且a≠-2 |
下列结论中,不正确的是()
A.方程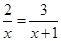 的解是 的解是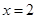 |
B.方程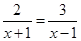 的解是 的解是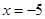 |
C.方程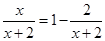 的解是 的解是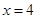 |
D.方程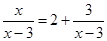 的解是 的解是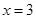 |
解分式方程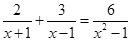 ,下列说法中错误的是()
,下列说法中错误的是()
A.方程两边分式的最简公分母是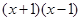 |
B.方程两边乘以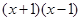 ,得整式方程 ,得整式方程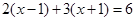 |
C.解这个整式方程,得 |
D.原方程的解为 |
下列说法中错误的是()
| A.分式方程的解等于0,就说明这个分式方程无解 |
| B.解分式方程的基本思路是把分式方程转化为整式方程 |
| C.检验是解分式方程必不可少的步骤 |
| D.能使分式方程的最简公分母等于零的未知数的值不是原分式方程的解. |