将下列各式因式分解：(本题10分)
（1）
（2）
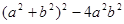
《九章算术》第九章的第九题为：今有圆材，埋在壁中，不知大小．以锯锯之，深一寸，锯道长一尺．问径几何．译成现代文并配图如下：圆木埋在壁中，不知大小，用锯子来锯它，锯到深度CD＝
cm时，量得锯痕AB＝
cm，问圆木的直径是多少cm?
如图，根据图像完成下列各题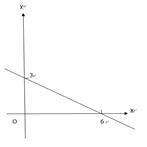
（1）当y=0时，x=；
（2）当x时，y<0；
（3）y随x的增大而；
（4）求函数解析式.
某电视台与某广告公司约定播放甲、乙两部电视剧，经调查，播放甲连续剧平均每集有观众20万人次，播放乙连续剧平均每集有观众15万人次，公司要求电视台每周共播放7集。
（1）设一周内甲连续剧播x集，甲、乙两部连续剧的观众总收视人数为y万人次，求y与x的函数关系式；
（2）已知电视台每周只能为该公司提供不超过300分钟的播放时间，并且播放甲连续剧每集50分钟，播放乙连续剧每集35分钟，问电视台每周应各播放甲、乙两种连续剧多少集，才能使每周收视观众的人数总和最大？并求出这个最大值。
已知一次函数y=x+2
（1）在平面直角坐标系内画出函数y=x+2的图像 ；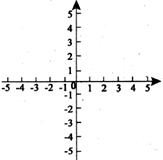
（2）求当x=2时，y的值；
已知，如图，在△ABC中，∠ACB=90°，AC=BC，BE⊥CE于点E，AD⊥CE于点D.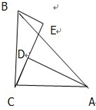
求证：△BEC≌△CDA．