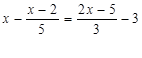阅读材料，并解答问题。
我们已经学过了一元一次不等式的解法，对于一些特殊的不等式，我们用作函数图象的方法求出它的解集，这也是《数学新课程标准》中所要求掌物的内容。例如：如何求不等式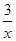
﹥x+2的解集呢？ 我们可以设
=,
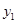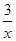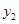=x+2.然后求出它们的交点的坐标， 并在同一直角坐标系中画出它们的函数图象，通过看图，可以发现此不等式的解集是“xく-3或0くxく1” 用上面的知识解决问题：求不等式x
-x＞x+3的解集.
（1）设函数= ， =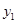
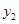(2)两个函数图象的交点坐标为
（3）在所给的直角坐标系中画出两个函数的图象（不要列表）.
（4）观察发现：不等式x-x＞x+3的解集为 
如图，⊙O的半径OB＝5 cm，AB是⊙O的弦，点C是AB延长线上一点，且∠OCA＝30°，OC＝8 cm，求AB的长．
如图，已知△ABC的三个顶点的坐标分别 为A（-6，0）、B（-2，3）、C（-1，0）．
（1）将△ABC绕坐标原点O逆时针旋转90°．画出对应的△A′B′C′图形；
（2）若四边形A′B′C′D′为平行四边形，请直接写出第四个顶点D′的坐标．
（每小题6分共12分）解方程
（1）2（x+2）2－8="0" ；
（2）2x2-7x+3=0．
如图，点E、D、F在同一条直线上，∠CDE=90°，∠1=∠2．
哪些角互为余角？哪些角互为补角？
∠ADC和∠BDC有什么关系？为什么？
∠ADF和∠BDE有什么关系？为什么？
解方程（每题4分，共8分）
（1）
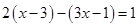
（2）