某政府大力扶持大学生创业.李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯.物价部门规定,这种护眼台灯的销售单价不得高于32元.销售过程中发现,月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:y=-10x+n.
(1)当销售单价x定为25元时,李明每月获得利润为w为1250元,则n= ;
(2)如果李明想要每月获得2000元的利润,那么销售单价应定为多少元?
(3)当销售单价定为多少元时,每月可获得最大利润?并求最大利润为多少元.
(·辽宁锦州)2015年5月,某校组织了以“德润书香”为主题的电子小报制作比赛,评分结果只有60,70,80,90,100五种,现从中随机抽取部分作品,对其份数和成绩进行整理,制成如下两幅不完整的统计图: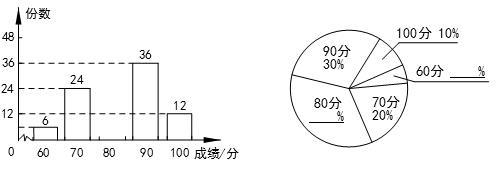
根据以上信息,解答下列问题:
(1)求本次抽取了多少份作品,并补全两幅统计图;
(2)已知该校收到参赛作品共900份,比赛成绩达到90分以上(含90分)的为优秀作品,据此估计该校参赛作品中,优秀作品有多少份?
(·辽宁本溪)某中学为开拓学生视野,开展“课外读书周”活动,活动后期随机调查了九年级部分学生一周的课外阅读时间,并将结果绘制成两幅不完整的统计图,请你根据统计图的信息回答下列问题: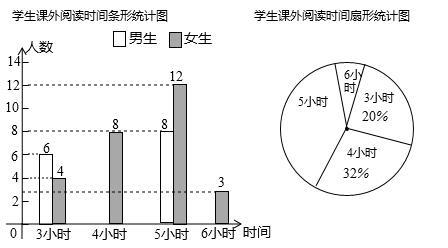
(1)本次调查的学生总数为 人,被调查学生的课外阅读时间的中位数是 小时,众数是 小时;
(2)请你补全条形统计图;
(3)在扇形统计图中,课外阅读时间为5小时的扇形的圆心角度数是 ;
(4)若全校九年级共有学生700人,估计九年级一周课外阅读时间为6小时的学生有多少人?
(·吉林长春)在“世界家庭日”前夕,某校团委随机抽取了 名本校学生,对“世界家庭日”当天所喜欢的家庭活动方式进行问卷调查,问卷中的家庭活动方式包括:
名本校学生,对“世界家庭日”当天所喜欢的家庭活动方式进行问卷调查,问卷中的家庭活动方式包括:
A.在家里聚餐; B.去影院看电影;
C.到公园游玩 D.进行其他活动.
每位学生在问卷调查时都按要求只选择了其中一种喜欢的活动方式,该校团委收回全部调查问卷后,将收集到的数据整理并绘制成如下的统计图.根据统计图提供的信息,解答下列问题:
(1)求 的值;
的值;
(2)四种方式中最受学生喜欢的方式为 (用A、B、C、D作答);选择该种方式的学生人数占被调查的学生人数的百分比为 ;
(3)根据统计结果,估计该校1800名学生中喜欢C方式的学生比喜欢B方式的学生多的人数.
(·吉林长春)在一个不透明的袋子里装有3张卡片,卡片上面分别标有字母 ,每张卡片除字母不同外其他都相同,小玲先从盒子中随机抽出一张卡片,记下字母后放回并摇匀,再从盒子中随机抽出一张卡片记下字母,用画树状图(或列表)的方法,求小玲两次抽出的卡片上的字母相同的概率.
,每张卡片除字母不同外其他都相同,小玲先从盒子中随机抽出一张卡片,记下字母后放回并摇匀,再从盒子中随机抽出一张卡片记下字母,用画树状图(或列表)的方法,求小玲两次抽出的卡片上的字母相同的概率.
(·吉林省)要从甲、乙两名同学中选出一名,代表班级参加射击比赛,如图是两人最近10次射击训练成绩的折线统计图.
(1)已求得甲的平均成绩为8环,求乙的平均成绩;
(2)观察图形,直接写出甲,乙这10次射击成绩的方差 ,
, 哪个大;
哪个大;
(3)如果其他班级参赛选手的射击成绩都在7环左右,本班应该选 参赛更合适;如果其他班级参赛选手的射击成绩都在9环左右,本班应该选 参赛更合适.