一个容量为M的样本数据,其频率分布表如下.
(Ⅰ)完成频率分布表 ;
(Ⅱ)画出频率分布直方图 ;
(Ⅲ)利用频率分布直方图,估计总体的众数、中位数及平均数. 【解】 频率分布表 频率分布直方图
【解】 频率分布表 频率分布直方图
| 分组 |
频数 |
频率 |
| (10,20] |
2 |
0.10 |
| (20,30] |
3 |
|
| (30,40] |
4 |
0.20 |
| (40,50] |
|
|
| (50,60] |
4 |
0.20 |
| (60,70] |
2 |
0.10 |
| 合计 |
|
1.00 |
如图,已知四棱锥 ,
, ,
, ,
, 平面
平面 ,
, ∥
∥ ,
, 为
为 的中点.
的中点.
(1)求证: ∥平面
∥平面 ;
;
(2)求证:平面
 平面
平面 ;
;
(3)求四棱锥 的体积.
的体积.
某校高一(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如下图.

(1)求分数在 的频率及全班人数;
的频率及全班人数;
(2)求分数在 之间的频数,并计算频率分布直方图中
之间的频数,并计算频率分布直方图中 间矩形的高;
间矩形的高;
(3)若要从分数在 之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在
之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在 之间的概率.
之间的概率.
在△ 中,角
中,角 的对边分别为
的对边分别为 ,且
,且 ,
, .
.
(1)求角 的大小;
的大小;
(2)若 ,
, ,求
,求 边的长和△
边的长和△ 的面积.
的面积.
对于数列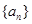 ,把
,把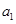 作为新数列
作为新数列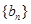 的第一项,把
的第一项,把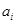 或
或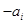 (
(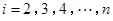 )作为新数列
)作为新数列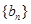 的第
的第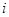 项,数列
项,数列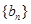 称为数列
称为数列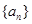 的一个生成数列.例如,数列
的一个生成数列.例如,数列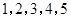 的一个生成数列是
的一个生成数列是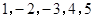 .已知数列
.已知数列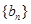 为数列
为数列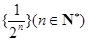 的生成数列,
的生成数列,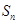 为数列
为数列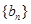 的前
的前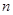 项和.
项和.
(1)写出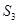 的所有可能值;
的所有可能值;
(2)若生成数列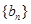 满足
满足 ,求数列
,求数列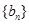 的通项公式;
的通项公式;
(3)证明:对于给定的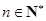 ,
,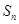 的所有可能值组成的集合为
的所有可能值组成的集合为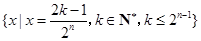 .
.
给定椭圆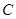 :
: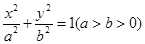 ,称圆心在原点
,称圆心在原点 ,半径为
,半径为 的圆是椭圆
的圆是椭圆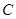 的“准圆”.若椭圆
的“准圆”.若椭圆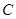 的一个焦点为
的一个焦点为 ,其短轴上的一个端点到
,其短轴上的一个端点到 的距离为
的距离为 .
.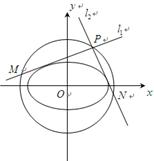
(1)求椭圆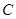 的方程和其“准圆”方程;
的方程和其“准圆”方程;
(2)点 是椭圆
是椭圆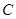 的“准圆”上的动点,过点
的“准圆”上的动点,过点 作椭圆的切线
作椭圆的切线 交“准圆”于点
交“准圆”于点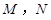 .
.
(ⅰ)当点 为“准圆”与
为“准圆”与 轴正半轴的交点时,求直线
轴正半轴的交点时,求直线 的方程,
的方程,
并证明 ;
;
(ⅱ)求证:线段 的长为定值.
的长为定值.