一个单摆在质量为m1、半径为R1的星球上做周期为T1的简谐运动,在质量为m2、半径为R2的星球上做周期为T2的简谐运动,求T1与T2之比。
)(如图所示,质量分别为1 kg、3 kg的滑块A、B位于光滑水平面上,现使滑块A以4 m/s的速度向右运动,与左侧连有轻弹簧的滑块B发生碰撞.求二者在发生碰撞的过程中,
①弹簧的最大弹性势能;
②滑块B的最大速度。
)(由透明体做成的三棱柱,横截面为有一个锐角为300的直角三角形,如图乙所示,AC面镀膜,经透明体射到AC面的光只能反射。现有一束光从AB面的D点垂直AB面射入透明体,经AC面E点反射后从BC面射出透明体,出射光线与BC面成300角①求该透明体的折射率;
②若光线从BC面的F点垂直BC面射入透明体,经AC面E点反射后从AB面射出透明体,试画出经E点后的光路图,并标明出射光线与AB面所成夹角的角度(不用列式计算)。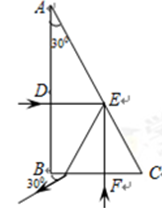
)(某同学用吸管吹出一球形肥皂泡,开始时,气体在口腔中的温度为37℃,吹出后的肥皂泡体积为0.5L,温度为0℃,肥皂泡内、外压强差别不大,均近似等于1个标准大气压。试估算肥皂泡内的气体分子个数和这部分气体在口腔内的体积。
分如图所示,在坐标系xOy内有一半径为a的圆形区域,圆心坐标为O1(a,0),圆内分布有垂直纸面向里的匀强磁场。在直线y=a的上方和直线x=2a的左侧区域内,有一沿y轴负方向的匀强电场,场强大小为E.一质量为m、电荷量为+q(q>0)的粒子以速度v从O点垂直于磁场方向射入,当速度方向沿x轴正方向时,粒子恰好从O1点正上方的A点射出磁场,不计粒子重力。
⑴求磁感应强度B的大小;
⑵粒子在第一象限内运动到最高点时的位置坐标;
⑶若粒子以速度v从O点垂直于磁场方向射入第一象限,当速度方向沿x轴正方向的夹角 =30°时,求粒子从射入磁场到最终离开磁场的时间t.
=30°时,求粒子从射入磁场到最终离开磁场的时间t.
分如图所示,光滑圆弧轨道最低点与光滑斜面在B点用一段光滑小圆弧平滑连接,可认为没有能量的损失,圆弧半径为R=0.5m,斜面的倾角为450,现有一个可视为质点、质量为m=0.1kg的小球从斜面上A点由静止释放,通过圆弧轨道最低点B时对轨道的压力为6N.以B点为坐标原点建立坐标系如图所示(g=l0m/s2)求:
(1)小球最初自由释放位置A离最低点B的高度h.
(2)小球运动到C点时对轨道的压力的大小;
(3)小球从离开C点至第一次落回到斜面上,落点的坐标是多少?