如图所示,在光滑的水平地面上,静止着质量为M =2.0kg的小车A,小车的上表面距离地面的高度为0.8m,小车A的左端叠放着一个质量为m=1.0kg的小物块B(可视为质点)处于静止状态,小物块与小车上表面之间的动摩擦因数μ=0.20。在小车A的左端正上方,用长为R=1.6m的不可伸长的轻绳将质量为m =1.0kg的小球C悬于固定点O点。现将小球C拉至使轻绳拉直且与竖起方向成θ=60°角的位置由静止释放,到达O点的正下方时,小球C与B发生弹性正碰(碰撞中无机械能损失),小物块从小车右端离开时车的速度为1m/s,空气阻力不计,取g=10m/s2. 求: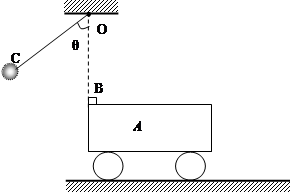
(1)小车上表面的长度L是多少?
(2)小物块落地时距小车右端的水平距离是多少?
某压力锅结构如图所示。盖好密封锅盖,将压力阀套在出气孔上,给压力锅加热,当锅内气体压强达到一定值时,气体就把压力阀顶起。假定在压力阀被顶起时,停止加热。
(1)若此时锅内气体的体积为V,摩尔体积为V0,阿伏加德罗常数为NA,写出锅内气体分子数的估算表达式。
(2)假定在一次放气过程中,锅内气体对压力阀及外界做功1 J,并向外界释放了2 J的热量。锅内原有气体的内能如何变化?变化了多少?
(3)已知大气压强P随海拔高度H的变化满足P=P0(1-αH),其中常数α>0。结合气体定律定性分析在不同的海拔高度使用压力锅,当压力阀被顶起时锅内气体的温度有何不同。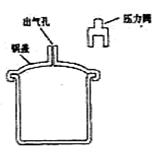
一定质量的理想气体由状态A变为状态B,其中A B过程为等压变化。已知VA=0.3m3,TA= 300K、TB=400K。求气体在状态B时的体积。
B过程为等压变化。已知VA=0.3m3,TA= 300K、TB=400K。求气体在状态B时的体积。
如图所示,两平行金属板A、B长l=8cm,两板间距离d=8cm,A板比B板电势高300V,即UAB=300V.一带正电的粒子电量q=10-10C,质量m=10-20kg,从R点沿电场中心线垂直电场线飞入电场,初速度v0=2×106m/s,粒子飞出平行板电场后经过界面MN、PS间的无电场区域后,进入固定在中心线上O点的点电荷Q形成的电场区域(设界面PS右边点电荷的电场分布不受界面的影响).已知两界面MN、PS相距为L=12cm,粒子穿过界面PS最后垂直打在放置于中心线上的荧光屏EF上.(静电力常数k=9×109N・m2/C2)求
(1)粒子穿过界面MN时的速度;
(2)粒子穿过界面PS时偏离中心线RO的距离多远;
(3)点电荷的电量.
如图所示,斜面轨道AB与水平面之间的夹角θ=53O,BD为半径R =" 4" m的圆弧形轨道,且B点与D点在同一水平面上,在B点,轨道AB与圆弧形轨道BD相切,整个轨道处于竖直平面内且处处光滑,在A点处的一质量m=1kg的小球由静止滑下,经过B、C点后从D点斜抛出去,最后落在地面上的S点处时的速度大小vS= 8m/s,已知A点距地面的高度H = 10m,B点距地面的高度h ="5" m,设以MDN为分界线,其左边为一阻力场区域,右边为真空区域,g取10m/s2, ,
,
(1)小球经过C点的速度为多大?
(2)小球从D点抛出后,受到的阻力f与其瞬时速度方向始终相反,求小球从D点至S点的过程中,阻力f所做的功.
如图所示电路,U恒为10V、R1=4Ω、R2=6Ω、C1=C2=30μF,先闭合开关S,待电路稳定后再断开S,求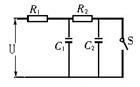
(1)闭合开关S稳定后,C1上的电量;
(2)断开开关S稳定后,C2上的电量
(3)从闭合S稳定到断开S稳定过程中,通过电阻R2、R1的电荷量.