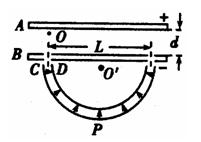
两根相距L=0.5m的足够长的金属导轨如图甲所示放置,他们各有一边在同一水平面上,另一边垂直于水平面。金属细杆ab、cd的质量均为m=0.05kg,电阻均为R=1.0Ω,它们与导轨垂直接触形成闭合回路,杆与导轨之间的动摩擦因数μ=0.5,导轨电阻不计。整个装置处于磁感应强度大小B=1.0T、方向竖直向上的匀强磁场中。当ab杆在平行于水平导轨的拉力F作用下沿导轨向右运动时,从某一时刻开始释放cd杆,并且开始计时,cd杆运动速度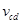 随时间变化的图像如图乙所示(在0~1s和2~3s内,对应图线为直线。g=10m/s2)。求:
随时间变化的图像如图乙所示(在0~1s和2~3s内,对应图线为直线。g=10m/s2)。求:


(1)在0~1s时间内,回路中感应电流I1的大小;
(2)在0~3s时间内,ab杆在水平导轨上运动的最大速度Vm;
(3)已知1~2s内,ab杆做匀加速直线运动,写出1~2s内拉力F随时间t变化的关系式,并在图丙中画出在0~3s内,拉力F随时间t变化的图像。(不需要写出计算过程,只需写出表达式和画出图线)
如图所示,在光滑水平面AB上,水平恒力F推动质量为m=1kg的物体从A点由静止开始作匀加速直线运动,物体到达 B点时撤去 F,接着又冲上光滑斜面(设经过B点前后速度大小不变),最高能到达C点。用速度传感器测量物体的瞬时速度,并在表格中记录了部分测量数据。求:(g取10m/s2)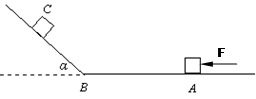
| t/s |
0.0 |
0.2 |
0.4 |
… |
2.2 |
2.4 |
2.6 |
… |
| v/m•s-1 |
0.0 |
0.4 |
0.8 |
… |
3.0 |
2.0 |
1.0 |
… |
(1)恒力F 的大小;
(2)斜面的倾角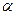 ;
;
(3)若撤去推力F,在A处给物体一个水平向左的初速度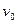 ,恰能使物体运动到C点,求此初速度
,恰能使物体运动到C点,求此初速度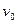 的大小。
的大小。
如图所示,在水平桌面上放有长木板C,C上右端是固定挡板P,在C上左端和中点处各放有小物块A和B,A、B的尺寸以及P的厚度皆可忽略不计,A、B之间和B、P之间的距离都为L.设木板C和桌面之间无摩擦,A、C和B、C之间的动摩擦因数都为μ,最大静摩擦力等于滑动摩擦力大小,A、B、C(连同挡板P)的质量都为m,开始时,B和C静止,A以某一初速度v0向右运动.求:
(1)A和B发生碰撞前,B受到的摩擦力大小?
(2)A和B能够发生碰撞时,A的初速度v0应满足的条件?
(3)B和P能够发生碰撞时,A的初速度v0应满足的条件?(已知A、B碰撞无机械能损失.)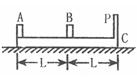
在农村人们盖房打地基叫打夯,夯锤的结构如图10所示,打夯共有5人,四个人分别握住夯锤的一个把手,一个人负责喊号,喊号人一声号子,四个人同时向上用力竖直将夯锤提起,号音一落四人同时松手,夯锤落至地面将地基砸实。某次打夯时,设夯锤的质量为80kg,将夯锤提起时,每个人都对夯锤施加竖直向上的力,大小均为250N,力的持续时间为0.6s,然后松手。夯锤落地时将地面砸出2cm深的一个凹痕。求:
(1)四个人松手瞬间夯锤的速度?
(2)夯锤能够上升的最大高度?
(3)夯锤落地时对地面的作用力为多大?(g=10m/s2)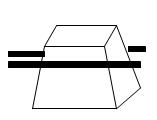
山地滑雪是人们喜爱的一项体育运动.一滑雪坡由AB和BC组成,AB是倾角为37°的斜坡,BC是半径为R=5m的圆弧面,圆弧面和斜面相切于B,与水平面相切于C,如图所示,AB竖直高度差hl=8.8m,竖直台阶CD高度差为h2=5m,台阶底端与倾角为37°斜坡DE相连.运动员连同滑雪装备总质量为80kg,从A点由静止滑下通过C点后飞落到DE上(不计空气阻力和轨道的摩擦阻力,g取10m/s2,sin37°=0.6,cos37°=0.8).求:
(1)运动员到达C点的速度大小?
(2)运动员经过C点时轨道受到的压力大小?
(3)运动员在空中飞行的时间?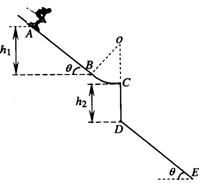
如图13所示,A、B为两块平行金属板,A板带正电,B板带负电。两板之间存在着匀强电场,两板间距为d,两板间电势差为U,在B板上开有两个间距为L的小孔。C、D为两块同心半圆形金属板,圆心都在贴近B板的Oˊ处,C带正电,D带负电。两半圆形金属板间的距离很近,两半圆形金属板末端的中心线正对着B板上的小孔,两半圆形金属板间的电场强度可认为大小处处相等,方向都指向Oˊ。半圆形金属板两端与B板的间隙可忽略不计。现从正对B板小孔、紧靠A板的O处由静止释放一个质量为m、电荷量为q的带正电微粒(微粒的重力不计)。求:
(1)微粒穿过B板小孔时的速度为多大;
(2)为了使微粒能在CD板间运动而不碰板,CD板间的电场强度大小应满足什么条件;
(3)在满足(2)的情况下,从释放微粒开始,经过多长时间微粒会通过半圆形金属板间的最低点P。