随着我市近几年城市园林绿化建设的快速发展,对花木的需求量逐年提高。某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润y1与投资成本x成正比例关系,如图①所示;种植花卉的利润y2与投资成本x成二次函数关系,如图②所示(注:利润与投资成本的单位:万元)
(1)分别求出利润y1与y2关于投资量x的函数关系式;
(2)如果这位专业户计划以8万元资金投入种植花卉和树木,请求出他所获得的总利润Z与投入种植花卉的投资量x之间的函数关系式,并回答他至少获得多少利润?他能获取的最大利润是多少?
如图,正比例函数 的图象与反比例函数
的图象与反比例函数 的图象分别交于M,N两点,已知点M(-2,m).
的图象分别交于M,N两点,已知点M(-2,m).
(1)求反比例函数的表达式;
(2)点P为y轴上的一点,当∠MPN为直角时,直接写出点P的坐标.
如图,矩形ABCD中,AP平分∠DAB,且AP⊥DP于点P,联结CP,如果AB﹦8,AD﹦4,求sin∠DCP的值.
已知二次函数 .
.
(1)把这个二次函数化成 的形式;
的形式;
(2)画出这个二次函数的图象,并利用图象写出当x为何值时, .
.
如图,已知抛物线 与x轴的一个交点为A(-1,0),另一个交点为B,与y轴的交点为C(0,-3),其顶点为D,对称轴为直线
与x轴的一个交点为A(-1,0),另一个交点为B,与y轴的交点为C(0,-3),其顶点为D,对称轴为直线 .
.
(1)求抛物线的解析式;
(2)已知点M为y轴上的一个动点,当△ACM是以AC为一腰的等腰三角形时,求点M的坐标;
(3)将△OBC沿x轴向右平移m个单位长度(0<m<3)得到另一个三角形△EFG,将△EFG与△BCD重叠部分的面积记为S,用含m的代数式表示S.
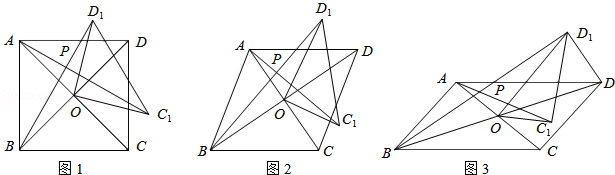
在四边形ABCD中,对角线AC、BD相交于点O,将△COD绕点O按逆时针方向旋转得到△C1OD1,旋转角为θ(0°<θ<90°),连接AC1、BD1,AC1与BD1交于点P.
(1)如图1,若四边形ABCD是正方形.
①求证:△AOC1≌△BOD1.
②请直接写出AC1与BD1的位置关系.
(2)如图2,若四边形ABCD是菱形,AC=5,BD=7,设AC1=kBD1.判断AC1与BD1的位置关系,说明理由,并求出k的值.
(3)如图3,若四边形ABCD是平行四边形,AC=5,BD=10,连接DD1,设AC1=kBD1.请直接写出k的值和 的值.
的值.