(本小题满分10分)从 名男生和
名男生和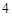 名女生中选出
名女生中选出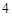 人参加学校辩论赛.
人参加学校辩论赛.
(Ⅰ)如果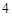 人中男生和女生各选
人中男生和女生各选 人,有多少种选法?
人,有多少种选法?
(Ⅱ)如果男生中的甲和女生中的乙至少有1人在内,有多少种选法?
已知
,且
是第一象限.
(1)求
的值;
(2)求
的值.
已知函数f(x)=sinx+cosx.
(1)若f(x)=2f(﹣x),求 的值;
的值;
(2)求函数F(x)=f(x)•f(﹣x)+f2(x)的最大值和单调递增区间.
在数列{an}中,a1=1,an+1=2an+2n.
(1)设bn= ,证明:数列{bn}是等差数列;
,证明:数列{bn}是等差数列;
(2)求数列{an}的前n项和Sn,
(3)设cn= ,求数列{cn}的最大项.
,求数列{cn}的最大项.
已知函数y=f(x)=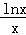 .
.
(1)求函数y=f(x)的图象在x= 处的切线方程;
处的切线方程;
(2)求y=f(x)的最大值;
(3)设实数a>0,求函数F(x)=af(x)在[a,2a]上的最小值.
命题p:关于x的不等式x2+2ax+4>0,对一切x∈R恒成立,命题q:指数函数f(x)=(3﹣2a)x是增函数,若p∨q为真,p∧q为假,求实数a的取值范围.