观察下列等式:
12×231=132×21,
13×341=143×31,
23×352=253×32,
34×473=374×43,
62×286=682×26,
…
以上每个等式中两边数字是分别对称的,且每个等式中组成两位数与三位数的数字之间具有相同规律,我们称这类等式为“数字对称等式”.
(1)根据上述各式反映的规律填空,使式子称为“数字对称等式”:
①52× = ×25;
② ×396=693× .
(2)设这类等式左边两位数的十位数字为a,个位数字为b,且2≤a+b≤9,写出表示“数字对称等式”一般规律的式子(含a、b),并证明.
在△ABC中,AB=AC=5,BC=6,求cosB、sinA.
如图,已知O是坐标原点,B、C两点的坐标分别为(3,–1)、(2,1) .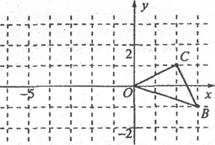
(1)以0点为位似中心在y轴的左侧将△OBC放大到两倍(即新图与原图的相似比为2),画出图形;
(2)分别写出B、C两点的对应点B′、C′的坐标;
如图:已知△ABC为等腰直角三角形,∠ACB=90°,延长BA至E,延长AB至F,∠ECF=135°
求证:△EAC∽△CBF
清明节期间,某中学团委组织八年级部分学生去离校2.4千米的某烈士陵园扫墓,回来时乘公交车所花时间比去时步行少用了36分钟,已知公交车速度是学生步行速度的5倍,求学生的步行速度.
有一道题“先化简,再求值: .其中a =-5”马小虎同学做题时把“a = -5”错抄成了“a =5”,但他的计算结果却与别的同学一致,也是正确的,请你解释这是怎么回事?
.其中a =-5”马小虎同学做题时把“a = -5”错抄成了“a =5”,但他的计算结果却与别的同学一致,也是正确的,请你解释这是怎么回事?