某项新技术进入试用阶段前必须对其中三项不同指标甲、乙、丙进行通过量化检测。假设该项新技术的指标甲、乙、丙独立通过检测合格的概率分别为 ,指标甲、乙、丙检测合格分别记4分、2分、4分,若某项指标不合格,则该项指标记0分,各项指标检测结果互不影响。
,指标甲、乙、丙检测合格分别记4分、2分、4分,若某项指标不合格,则该项指标记0分,各项指标检测结果互不影响。
(Ⅰ)求该项技术量化得分不低于8分的概率;
(Ⅱ)记该技术的三个指标中被检测合格的指标个数为随机变量 ,求
,求 的分布列与数学期望。
的分布列与数学期望。
(本小题满分12分)
有编号为l,2,3,……, 的
的 个学生,入坐编号为1,2,3,……,
个学生,入坐编号为1,2,3,……, 的
的 个座位.每个学生规定坐一个座位,设学生所坐的座位号与该生的编号不同的学生人数为
个座位.每个学生规定坐一个座位,设学生所坐的座位号与该生的编号不同的学生人数为 ,已知
,已知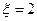 时,共有6种坐法.
时,共有6种坐法.
(1)求 的值;
的值;
(2)求随机变量 的概率分布列和数学期望.
的概率分布列和数学期望.
(本小题满分10分)
若函数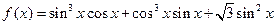 .
.
(1)求函数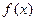 的单调递减区间;
的单调递减区间;
(2)已知 的三边
的三边 、
、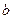 、
、 对应角为
对应角为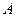 、
、 、
、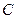 ,且三角形的面积为
,且三角形的面积为 ,若
,若 ,求
,求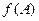 的取值范围.
的取值范围.
我国计划发射火星探测器,该探测器的运行轨道是以火星(其半径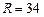 百公里)的中心
百公里)的中心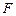 为一个焦点的椭圆
为一个焦点的椭圆 . 如图,已知
. 如图,已知 探测器的近火星点(轨道上离火星表
探测器的近火星点(轨道上离火星表 面最近的点)
面最近的点)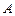 到火星表面的距离为
到火星表面的距离为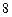 百公里,远火星点(轨道上离火星表面最远的点)
百公里,远火星点(轨道上离火星表面最远的点)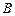 到火星表面的距离为800百公里. 假定探测器由近火星点
到火星表面的距离为800百公里. 假定探测器由近火星点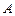 第一次逆时针运行到与轨道中心
第一次逆时针运行到与轨道中心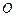 的距离为
的距离为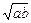 百公里时进行变轨,其中
百公里时进行变轨,其中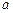 、
、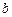 分别为椭圆的长半轴、短半轴的长,求此时探测器与火星表面的距离(精确到1百公里).
分别为椭圆的长半轴、短半轴的长,求此时探测器与火星表面的距离(精确到1百公里).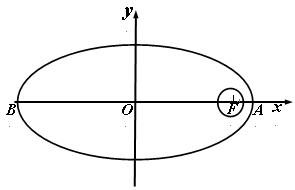
已知点(x, y)是曲线C上任意一点,将此点的纵坐标变为原来的2倍,对应的横坐标不变,得到的点满足方程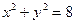 ;定点M(2,1),平行于OM的直线
;定点M(2,1),平行于OM的直线
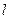 在y轴上的截距为m(m≠0),直线
在y轴上的截距为m(m≠0),直线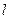 与曲线C交于A、B两个不同点.
与曲线C交于A、B两个不同点.
(1)求曲线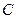 的方程;
的方程;
(2)求 m的取值范围.
m的取值范围.
已知函数
 ,
, .
.
(1)求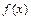 的最大值和最小值;
的最大值和最小值;
(2)若不等式 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.