（本小题满分12分）
在锐角
中，内角
对边的边长分别是
，且
,
（Ⅰ）求角
；
（
Ⅱ）若边
， 的面积等于
， 求边长
和
.
（本小题满分12分）
设数列
为等差数列，前
项和为
，已知
，
，
（Ⅰ）求的通项公式；
（Ⅱ）若
，求数列
的前项和
.
（本小题满分12分）
已知命题
：关于
的不等式
的解集为空集
；命题
：函数
为增函数，若命题
为假命题，
为真命题，求实数
的取值范围.
本小题满分12分）
设函数
若不等式
的解集是
，求不等式
的解集.
（本小题满分14分）
已知椭圆中心在原点，焦点在x轴上，离心率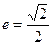
，过椭圆的右焦点且垂直于长轴的弦长为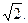
（1）求椭圆的标准方程；
（2）已知直线l与椭圆相交于P、Q两点，O为原点，
且OP⊥OQ。试探究点O到直线l的距离是否为定值？若是，求出这个定值；若不是，说明理由。
中，
平面
，底面
.
时，求证：
；
边上有且只有一个点
，使得
，求此时二面角
的余弦值.