某时刻海上点P处有一客轮,测得灯塔A位于客轮P的北偏东30°方向,且相距20海里.客轮以60海里/小时的速度沿北偏听偏西60°方向航行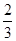 小时到达B处,那么tan∠ABP=【 】
小时到达B处,那么tan∠ABP=【 】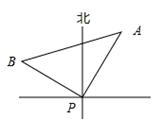
A.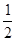 |
B.2 | C.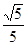 |
D.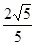 |
如图所示,△FDE经过怎样的平移可得到△ABC.( )
A.沿射线EC的方向移动DB长 B.沿射线EC的方向移动CD长
C.沿射线BD的方向移动BD长 D.沿射线BD的方向移动DC长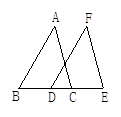
如图,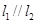 ,A、B为直线
,A、B为直线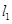 上两点,C、D为直线
上两点,C、D为直线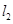 上两点,则
上两点,则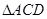 与
与 的面积大小关系是()
的面积大小关系是()
A、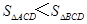 B、
B、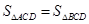 C、
C、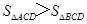 D、不能确定
D、不能确定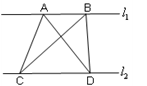
已知:如图,l1∥l2,∠1=50°, 则∠2的度数是()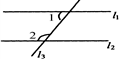
| A.135° | B.130° | C.50° | D.40° |
两条不平行的直线被第三条直线所截,下列说法可能成立的是()
| A.同位角相等 | B.内错角相等 | C.同旁内角相等 | D.同旁内角互补 |
下列命题正确的是()
| A.若两个角相等,则这两个角是对顶角 | B.若两个角是对顶角,则这两个角不等 |
| C.若两个角是对顶角,则这两个角相等 | D.所有同顶点的角都相等 |