对数列 ,如果
,如果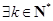 及
及 ,使
,使 成立,其中
成立,其中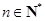 ,则称
,则称 为
为 阶递归数列.给出下列三个结论:
阶递归数列.给出下列三个结论:
① 若 是等比数列,则
是等比数列,则 为
为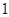 阶递归数列;
阶递归数列;
② 若 是等差数列,则
是等差数列,则 为
为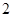 阶递归数列;
阶递归数列;
③ 若数列 的通项公式为
的通项公式为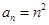 ,则
,则 为
为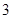 阶递归数列.
阶递归数列.
其中正确结论的个数是( )
| A.0 | B.1 | C.2 | D.3 |
若点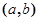 在函数
在函数 的图像上,且
的图像上,且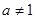 , 则下列点也在此函数图像上的是()
, 则下列点也在此函数图像上的是()
A.(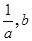 ) ) |
B.(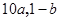 ) ) |
C.( , ,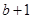 ) ) |
D.(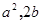 ) ) |
将函数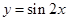 的图像向左平移
的图像向左平移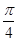 个单位,再向上平移
个单位,再向上平移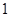 个单位,所得图像的函数解析式是()
个单位,所得图像的函数解析式是()
A.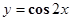 |
B.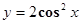 |
C.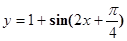 |
D.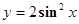 |
下列命题中,真命题是()
A.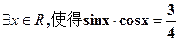 ; ; |
B.命题“若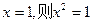 ”的逆命题; ”的逆命题; |
C.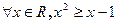 ; ; |
D.命题“若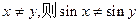 ”的逆否命题; ”的逆否命题; |
已知集合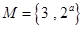 ,
,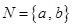 ,若
,若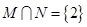 ,则
,则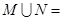 ()
()
A.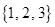 |
B. |
C.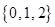 |
D.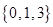 |
设a,b,c为实数 ,
,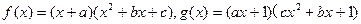 .记集合
.记集合 ,若
,若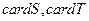 分别为集合S,T的元素个数,则下列结论不可能的是()
分别为集合S,T的元素个数,则下列结论不可能的是()
| A.cardS="1," cardT="0" | B.cardS="1," cardT=1 |
| C.cardS="2," cardT="2" | D.cardS="2,"  cardT=3 cardT=3 |