请你在下面3个网格(两相邻格点的距离均为1个单位长度)内,分别设计1个图案,要求:在图(1)中所设计的图案是面积等于 的轴对称图形;在图(2)中所设计的图案是面积等于2
的轴对称图形;在图(2)中所设计的图案是面积等于2 的中心对称图形;在图(3)中所设计的图案既是轴对称图形又是中心对称图形,并且面积等于3
的中心对称图形;在图(3)中所设计的图案既是轴对称图形又是中心对称图形,并且面积等于3 .将你设计的图案用铅笔涂黑.
.将你设计的图案用铅笔涂黑.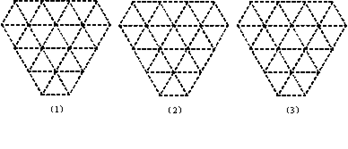
问题探究:
(1)请你在图①中做一条直线,使它将矩形 分成面积相等的两部分;
(2)如图②,点 是矩形 内一点,请你在图②中过 点作一条直线,使它将矩形 分成面积相等的两部分.
问题解决:
(3)如图③,在平面直角坐标系 中,多边形 的顶点坐标分别是 .若直线 经过点 ,且将多边形 分割成面积相等的两部分,求直线 的函数表达式.

如图,四边形 是正方形 的内接四边形, 与 都是锐角,已知 ,四边形 的面积为 .求正方形 的面积.

如图,四边形 是 的内接四边形。
(1)若 或 ,求证 ;
(2)若 ,问是否能推出 或 ?证明你的结论.

如图,已知 的面积分别为 , , , ,求 .

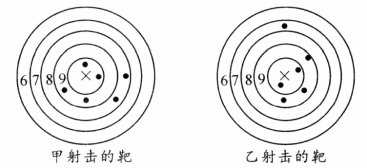
如图是甲、乙在一次射击比赛中击中靶的情况(击中靶中心的圆面为 环,靶中各数字表示该数所在圆环被击中所得的环数),每人射击了 次.
(1)请用列表法将他俩射击的成绩统计出来;
(2)请你用学过的统计知识,对他们的 次射击情况进行比较.