阅读下列材料:
正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫格点三角形.
数学老师给小明同学出了一道题目:在图正方形网格(每个小正方形边长为1)中画出格点△ABC,使 ,
, ;
;
小明同学的做法是:由勾股定理,得 ,
, ,于是画出线段AB、AC、BC,从而画出格点△ABC.
,于是画出线段AB、AC、BC,从而画出格点△ABC.
(1)请你参考小明同学的做法,在图中的正方形网格(每个小正方形边长为1)中画出格点△ (
( 点位置如图所示),使
点位置如图所示),使 =
= =5,
=5, .(直接画出图形,不写过程);
.(直接画出图形,不写过程);
(2)观察△ABC与△ 的形状,猜想∠BAC与∠
的形状,猜想∠BAC与∠ 有怎样的数量关系,并证明你的猜想.
有怎样的数量关系,并证明你的猜想. 

已知抛物线 经过点A(3,0),B(-1,0).
经过点A(3,0),B(-1,0).
(1)求抛物线的解析式;
(2)求抛物线的对称轴.
如图,在直角坐标系xoy中,O是坐标原点,点A在x正半轴上,OA=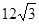 cm,点B在y轴的正半轴上,OB=12cm,动点P从点O开始沿OA以
cm,点B在y轴的正半轴上,OB=12cm,动点P从点O开始沿OA以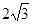 cm/s的速度向点A移动,动点Q从点A开始沿AB以4cm/s的速度向点B移动,动点R从点B开始沿BO以2cm/s的速度向点O移动.如果P、Q、R分别从O、A、B同时移动,移动时间为t(0<t<6)s.
cm/s的速度向点A移动,动点Q从点A开始沿AB以4cm/s的速度向点B移动,动点R从点B开始沿BO以2cm/s的速度向点O移动.如果P、Q、R分别从O、A、B同时移动,移动时间为t(0<t<6)s.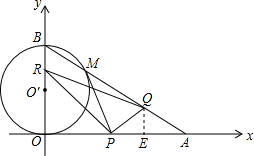
(1)求∠OAB的度数.
(2)以OB为直径的⊙O‘与AB交于点M,当t为何值时,PM与⊙O‘相切?
(3)求出△PQR的面积S随动点移动时间t的函数关系式,并求s的最小值及相应的t值.
某电子商投产一种新型电子产品,每件制造成本为18元,试销过程发现,每月销量
y(万件)与销售单价x(元)之间的关系可以近似地看作一次函数y=-2x+100.
(1)写出每月的利润z(万元)与销售单价x(元)之间函数解析式;
(2)当销售单价为 多少元时,厂商每月能够获得350万元的利润?当销售单价为多少元时,厂商每月能够获得最大利润?最大利润是多少?
(3)根据相关部门规定,这种电子产品的销售单价不得高于32元.如果厂商要获得每月不低于350万元的利润,那么制造这种产品每月的最低制造成本需要多少万元?
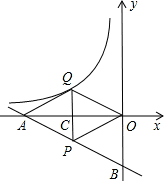
如图,一次函数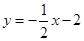 的图象分别交
的图象分别交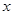 轴、
轴、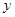 轴于
轴于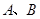 两点,
两点,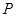 为
为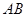 的中点,
的中点,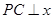 轴于点
轴于点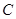 ,延长
,延长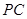 交反比例函数
交反比例函数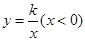 的图象于点
的图象于点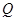 ,且
,且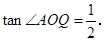
(1)求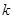 的值;
的值;
(2)连结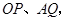 求证:四边形
求证:四边形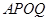 是菱形.
是菱形.
据统计某外贸公司2012年、2013年的进出口贸易总额分别为3300万元和3760万元, 其中2013年的进口和出口贸易额分别比2012年增长20%和10%.
(1)试确定2012年该公司的进口和出口贸易额分别是多少万元;
(2)2014年该公司的目标是:进出口贸易总额不低于4200万元, 其中出口贸易额所占比重不低于60%, 预计2014年的进 口贸易额比2013年增长10%, 则为完成上述目标,2014年的出口贸易额比2013年至少应增加多少万元?