(本小题满分12分)
为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系,下表记录了小李某月1号到5号每天打篮球时间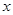 (单位:小时)与当天投篮命中率
(单位:小时)与当天投篮命中率 之间的关系:
之间的关系:
时间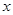 |
1 |
2 |
3 |
4 |
5 |
命中率 |
0.4 |
0.5 |
0.6 |
0.6 |
0.4 |
求小李这5天的平均投篮命中率;用线性回归分析的方法,预测小李该月6号打6小时篮球的投篮命中率.
附:线性回归方程 中系数计算公式
中系数计算公式 ,
, ,
,
(本小题满分10分) 已知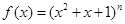 (
(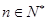 ),
),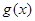 是关于
是关于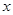 的
的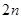 次多项式;
次多项式;
(1)若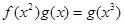 恒成立,求
恒成立,求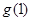 和
和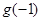 的值;并写出一个满足条件的
的值;并写出一个满足条件的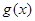 的表达式,无需证明.
的表达式,无需证明.
(2)求证:对于任意给定的正整数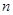 ,都存在与
,都存在与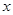 无关的常数
无关的常数 ,
,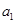 ,
,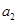 ,…,
,…,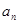 ,
,
使得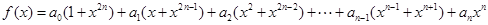 .
.
(本小题满分10分)某班组织的数学文化节活动中,通过抽奖产生了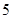 名幸运之星.这
名幸运之星.这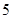 名幸运之星可获得
名幸运之星可获得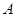 、
、 两种奖品中的一种,并规定:每个人通过抛掷一枚质地均匀的骰子决定自己最终获得哪一种奖品,抛掷点数小于
两种奖品中的一种,并规定:每个人通过抛掷一枚质地均匀的骰子决定自己最终获得哪一种奖品,抛掷点数小于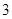 的获得
的获得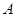 奖品,抛掷点数不小于
奖品,抛掷点数不小于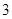 的获得
的获得 奖品.
奖品.
(1)求这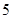 名幸运之星中获得
名幸运之星中获得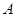 奖品的人数大于获得
奖品的人数大于获得 奖品的人数的概率;
奖品的人数的概率;
(2)设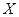 、
、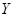 分别为获得
分别为获得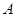 、
、 两种奖品的人数,并记
两种奖品的人数,并记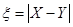 ,求随机变量
,求随机变量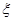 的分布列及数学期望.
的分布列及数学期望.
(本小题满分10分,不等式选讲)
已知不等式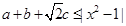 对于满足条件
对于满足条件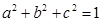 的任意实数
的任意实数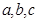 恒成立,求实数
恒成立,求实数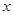 的取值范围.
的取值范围.
(本小题满分10分,坐标系与参数方程选讲)
已知极坐标系的极点与直角坐标系的原点重合,极轴与x轴的正半轴重合.若直线l的极坐标方程为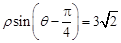 .
.
(1)把直线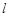 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)已知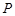 为椭圆
为椭圆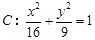 上一点,求
上一点,求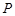 到直线
到直线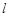 的距离的最小值.
的距离的最小值.
(本小题满分10分,矩阵与变换)
已知矩阵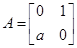 ,矩阵
,矩阵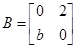 ,直线
,直线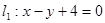 经矩阵
经矩阵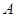 所对应的变换得到直线
所对应的变换得到直线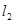 ,直线
,直线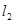 又经矩阵
又经矩阵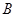 所对应的变换得到直线
所对应的变换得到直线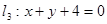 .
.
(1)求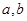 的值;(2)求直线
的值;(2)求直线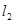 的方程.
的方程.