申请某种许可证,根据规定需要通过统一考试才能获得,且考试最多允许考四次. 设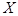 表示一位申请者经过考试的次数,据统计数据分析知
表示一位申请者经过考试的次数,据统计数据分析知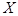 的概率分布如下:
的概率分布如下:
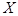 |
1 |
2 |
3 |
4 |
| P |
0.1 |
 |
0.3 |
0.1 |
(Ⅰ)求一位申请者所经过的平均考试次数;
(Ⅱ)已知每名申请者参加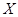 次考试需缴纳费用
次考试需缴纳费用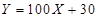 (单位:元),求两位申请者所需费用的和小于500元的概率;
(单位:元),求两位申请者所需费用的和小于500元的概率;
(Ⅲ)在(Ⅱ)的条件下, 4位申请者中获得许可证的考试费用低于300元的人数记为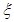 ,求
,求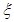 的分布列.
的分布列.