如果一条抛物线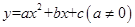 与
与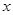 轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.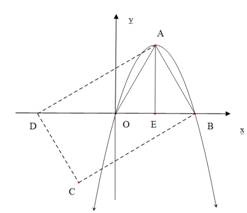
(1)“抛物线三角形”一定是 三角形;
(2)若抛物线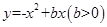 的“抛物线三角形”是等腰直角三角形,求
的“抛物线三角形”是等腰直角三角形,求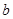 的值;
的值;
(3)如图,△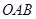 是抛物线
是抛物线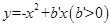 的“抛物线三角形”,是否存在以原点
的“抛物线三角形”,是否存在以原点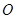 为对称中心的矩形
为对称中心的矩形 ?若存在,求出过
?若存在,求出过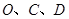 三点的抛物线的表达式;若不存在,说明理由.
三点的抛物线的表达式;若不存在,说明理由.
化简: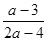 ÷(
÷(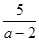 -a-2),并代入一个你喜欢的
-a-2),并代入一个你喜欢的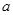 值求值.
值求值.
(1)计算:|-4|-( -1)0+2cos45°-(-
-1)0+2cos45°-(-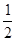 )-2+
)-2+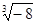
(2)解方程: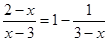
平面直角坐标系xOy中,抛物线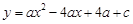 与x轴交于点A、点B,与y轴的正半轴交于点C,点 A的坐标为(1, 0),OB=OC,抛物线的顶点为D.
与x轴交于点A、点B,与y轴的正半轴交于点C,点 A的坐标为(1, 0),OB=OC,抛物线的顶点为D.
(1) 求此抛物线的解析式;
(2) 若此抛物线的对称轴上的点P满足∠APB=∠ACB,求点P的坐标;
(3) Q为线段BD上一点,点A关于∠AQB的平分线的对称点为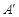 ,若
,若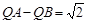 ,求点Q的坐标和此时△
,求点Q的坐标和此时△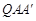 的面积.
的面积.
等边△ABC边长为6,P为BC边上一点,∠MPN=60°,且PM、PN分别于边AB、AC交于点E、F.(1)如图1,当点P为BC的三等分点,且PE⊥AB时,判断△EPF的形状;
(2)如图2,若点P在BC边上运动,且保持PE⊥AB,设BP=x,四边形AEPF面积的y,求y与x的函数关系式,并写出自变量x的取值范围;
(3)如图3,若点P在BC边上运动,且∠MPN绕点P旋转,当CF=AE=2时,求PE的长.
甲船从A港出发顺流匀速驶向B港,乙船同时从B港出发逆流匀速驶向A港.甲船行至某处,发现船上一救生圈不知何时落入水中,立刻原路返回,找到救生圈后,继续顺流驶向B港.已知甲、乙两船在静水中的速度相同,救生圈落入水中漂流的速度和水流速度都等于1.5km/h.甲、乙两船离A港的距离y1、y2(km)与行驶时间x(h)之间的函数图象如图所示.
(1)甲船在顺流中行驶的速度为km/h,m=;
(2)①当0≤x≤4时,求y2与x之间的函数关系式;
② 甲船到达B港时,乙船离A港的距离为多少?
(3)救生圈在水中共漂流了多长时间?