已知,如图,AB、DE是直立在地面上的两根立柱.AB=5m, 某一时刻AB在阳光下的投影BC=3m.
(1)请你在图中画出此时DE在阳光下的投影.
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为6m,请你计算DE的长.
地铁开通后,为响应市政府“绿色出行”的号召,家住沙区的小王上班由自驾车上班改为乘坐地铁.已知小王家距上班地点18千米,他用乘地铁的方式平均每小时行驶的路程比他用自驾车的方式平均每小时行驶的路程的2倍还多9千米,他从家出发到达上班地点,乘地铁所用时间是自驾车方式所用时间的 .小王用自驾车方式上班平均每小时行驶多少千米?
.小王用自驾车方式上班平均每小时行驶多少千米?
如图,反比例函数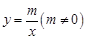 与一次函数
与一次函数 的图象交于点
的图象交于点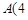 ,
,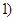 和点
和点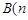 ,
,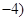 .
.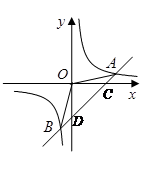
(1)求反比例函数和一次函数的解析式;
(2)求 的面积.
的面积.
先化简,再求值: ,其中
,其中 是不等式组
是不等式组 的整数解.
的整数解.
如图,四边形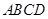 为菱形,已知
为菱形,已知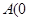 ,
,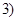 ,
,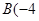 ,
,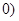 .(1)求点
.(1)求点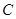 的坐标;
的坐标;
(2)求经过点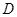 的反比例函数解析式.
的反比例函数解析式.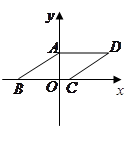
已知一次函数 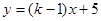 的图象经过点
的图象经过点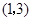 .
.
(1)求出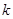 的值;
的值;
(2)求当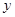 =1时,
=1时,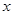 的值.
的值.