知识背景:恩施来凤有一处野生古杨梅群落,其野生杨梅是一种具特殊价值的绿色食品.在当地市场出售时,基地要求“杨梅”用双层上盖的长方体纸箱封装(上盖纸板面积刚好等于底面面积的2倍,如图)
实际运用:如果要求纸箱的高为0.5米,底面是黄金矩形(宽与长的比是黄金比,取黄金比为0.6),体积为0.3立方米.
①按方案1(如图)做一个纸箱,需要矩形硬纸板 的面积是多少平方米?
的面积是多少平方米?
②小明认为,如果从节省材料的角度考虑,采用方案2(如图)的菱形硬纸板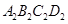 做一个纸箱比方案1更优,你认为呢?请说明理由.
做一个纸箱比方案1更优,你认为呢?请说明理由.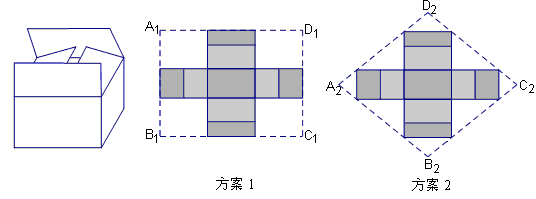
在某一地方,有条小河和草地,一天某牧民的计划是从A处的牧场牵着一只马到草地牧马,再到小河饮马,你能为他设计一条最短的路线吗?(在N上任意一点即可牧马,M上任意一点即可饮马.)(保留作图痕迹,需要证明)
如图,方格中有一个△ABC和直线l;
(1)请你在方格中画出△ABC关于直线l对称的△A1B1C1,并判断这两个三角形是否全等;(说出结论即可).
(2)请你在方格内,画出满足条件A1B1=AB,B1C1=BC,∠A1=∠A的△A2B2C2并判断△A2B2C2与△ABC是否一定全等.
△ABC的三边长分别为:AB=2a2﹣a﹣7,BC=1O﹣a2,AC=a,
(1)求△ABC的周长(请用含有a的代数式来表示);
(2)当a=2.5和3时,三角形都存在吗?若存在,求出△ABC的周长;若不存在,请说出理由;
(3)若△ABC与△DE成轴对称图形,其中点A与点D是对称点,点B与点E是对称点,EF=4﹣b2,DF=3﹣b,求a﹣b的值.
如图是小明用棋子摆成的字母“T”,它的主要特点是轴对称图形.请你再用棋子摆出两个轴对称图形的字母(用◯代表棋子).
如图1,A、B、C是三种不同型号的卡片,其中A型是边长为a的正方形,B型是长为b、宽为a的长方形,C是边长是b的正方形.
(1)小杰同学用1张A型、2张B型和1张C型卡片拼出了一个新的图形(如图2).请根据这个图形的面积关系写出一个你所熟悉的乘法公式,这个乘法公式是:.
(2)用第(1)小题中的四张卡片(全部用上)再拼出一个轴对称图形,且能利用这个图形的面积说明第(1)小题中你写出的乘法公式.请你画出这个轴对称图形.