小球在半径为R的光滑半球内做水平面内的匀速圆周运动,试分析图中的θ(小球与半球球心连线跟竖直方向的夹角)与线速度v、周期T的关系.(小球的半径远小于R)
某校课外活动小组,自制一枚土火箭,设火箭发射后,始终在垂直于地面的方向上运动。火箭点火后的加速阶段可认为做匀加速直线运动,经过4 s到达离地面40 m高处燃料恰好用完。(若空气阻力忽略不计,g取10m/s2)求:
(1)火箭上升离地面的最大高度是多大?
(2)火箭从发射到残骸落回地面的总时间是多大?
做匀加速直线运动的物体途中依次经过A、B、C三点,已知AB=BC= ,AB段和BC段的平均速度分别为= 3m/s、="6" m/s,则物体经B点时的瞬时速度为多大?
,AB段和BC段的平均速度分别为= 3m/s、="6" m/s,则物体经B点时的瞬时速度为多大?
如图,一质量m="5" kg的球被一光滑挡板夹在光滑墙上,保持静止。挡板与墙面接触且夹角为θ,满足θ=53°。求:挡板对球的支持力大小及球对墙面的压力大小?(计算时取sin53°=0.8,g=10m/s2)
将煤块A轻放在以2 m/s的恒定速度运动的足够长的水平传送带上后,传送带上留下一条长度为4 m的因相对运动而形成的擦痕.若使该传送带改做初速度不变、加速度大小为1.5 m/s2的匀减速运动直至速度为零,并且在传送带开始做匀减速运动的同时,将另一煤块B轻放在传送带上,g=10 m/s2,则:
(1).皮带与煤块间动摩擦因数μ为多少?
(2). 煤块B在皮带上的最长擦痕为多少?
(3). 煤块B停止在传送带上的位置与擦痕起点间的距离为多少?
如图所示,在倾角为θ=30°的固定斜面上,跨过定滑轮的轻绳一端系在小车的前端,另一端被坐在小车上的人拉住.已知人的质量为60 kg,小车的质量为10 kg,绳及滑轮的质量、滑轮与绳间的摩擦均不计,斜面对小车的摩擦阻力为人和小车总重力的0.1倍,取重力加速度g=10 m/s2,当人以280 N的力拉绳时,试求(斜面足够长):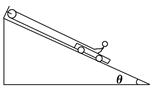
(1)人与车一起向上运动的加速度大小;
(2)人所受摩擦力的大小和方向;
(3)某时刻人和车沿斜面向上的速度为3 m/s,此时人松手,则人和车一起滑到最高点所用时间为多少?