14. (16分)在游乐节目中，选手需要借助悬挂在高处的绳飞越到水面的浮台上，小明和小阳观看后对此进行了讨论。如图所示，他们将选手简化为质量m=60kg的指点， 选手抓住绳由静止开始摆动，此事绳与竖直方向夹角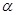
=
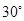，绳的悬挂点O距水面的高度为H=3m.不考虑空气阻力和绳的质量，浮台露出水面的高度不计，水足够深。取中立加速度
， 
，
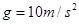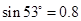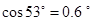
求（1）选手摆到最低点时对绳拉力的大小F；
（2）若绳长l="2m," 选手摆到最高点时松手落入手中。设水碓选手的平均浮力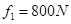
，平均阻力
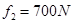，求选手落入水中的深度
；
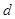（3）若选手摆到最低点时松手， 小明认为绳越长，在浮台上的落点距岸边越远；小阳认为绳越短，落点距岸边越远，请通过推算说明你的观点。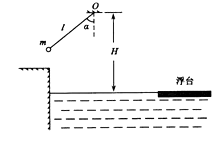
分如图，传送带与地面倾角θ=30°，AB长度为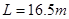
，传送带以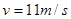
的速率逆时针转动。在传送带上端A无初速度地放上一个质量为
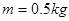的物体，它与传送带之间的动摩擦因数为
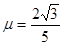，取
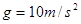，则：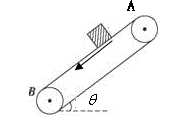
（1）从物体开始运动至物体刚与传送带达到共同速度这一过程中,传送带的摩擦力对物体做了多少功?
（2）物体从与传送带达到共同速度的瞬间至滑到B端的过程中，传送带的摩擦力对物体又做了多少功?
如图所示，轻杆长为3L， 在杆的A、B两端分别固定质量均为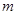
的球A和球B，杆上距球A为L处的点O装在光滑水平转动轴上，杆和球在竖直面内转动，已知球A运动到最高点时，球A对杆恰好无作用力。求：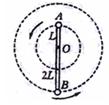 
（1）球A在最高点时的角速度大小；
（2）球A在最高点时，杆对水平轴的作用力的大小和方向。
如图所示，倾角θ=30°，高为h的三角形木块B，静止放在一水平面上，另一滑块A，以初速度v0从B的底端开始沿斜面上滑，若B的质量为A的质量的2倍，当忽略一切摩擦的影响时，要使A能够滑过木块B的顶端，求V0应为多大？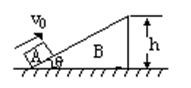
(１０分 )如图所示，扇形OAB为透明柱状介质的横截面，其圆柱半径为R，介质的
折射率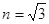
，圆心角∠AOB=60°，一细束激光平行于角平分线由OA面的P点射入，射入介质后第一次射到界面上的N点，已知弧长AN是弧长AB的四分之一。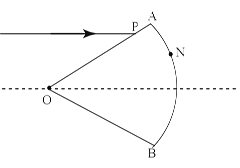
（1）完成光在透明柱状介质中传播的光路图
（2）求入射点P与圆心O的距离
如图所示，用导热性能良好的气缸和活塞封闭一定质量的理想气体，气体的体积V1=8.0×10﹣3m3，温度T1=4.0×102K．现使外界环境温度缓慢降低至T2，此过程中气体放出热量7.0×102J，内能减少了5.0×102J．不计活塞的质量及活塞与气缸间的摩擦，外界大气压强p0=1.0×105Pa．求T2的值．