过山车是游乐场中常见的设施。下图是一种过山车的简易模型，它由水平轨道和在竖直平面内的三个圆形轨道组成，B、C、D分别是三个圆形轨道的最低点，B、C间距与C、D间距相等，半径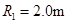
、
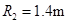。一个质量为
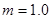kg的小球（视为质点），从轨道的左侧A点以
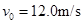的初速度沿轨道向右运动，A、B间距
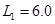m。小球与水平轨道间的动摩擦因数
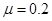，圆形轨道是光滑的。假设水平轨道足够长，圆形轨道间不相互重叠。重力加速度取
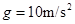，计算结果保留小数点后一位
数字。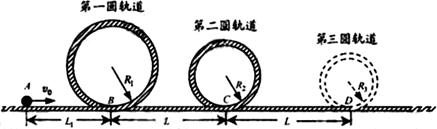
试求
（1）小球在经过第一个圆形轨道的最高点时，轨道对小球作用力的大小；
（2）如果小球恰能通过第二圆形轨道，B、C间距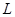
应是多少；
（3）在满足（2）的条件下，如果要使小球不能脱离轨道，在第三个圆形轨道的设计中，半径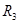
应满足的条件；小球最终停留点与起点
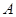的距离。
电动自行车是一种重要的交通工具，都市中每天有数十万辆电动自行车行驶在大街小巷，形成了一道独特的风景。电动自行车提供能量的装置为装在电池盒内的电池组，当它给电动机供电时，电动机将带动车轮转动。假设有一辆电动自行车，人和车的总质量为120kg。当该车在水平地面上以5m/s的速度匀速行驶时，它受到的阻力约等于人和车总重的0.02倍，此时电池组加在电动机两端的电压为36V，通过电动机的电流为5A。若连接导线的电阻不计，传动装置消耗的能量不计，g取10m/s2。求：
（1）电动机输出的机械功率
（2）电动机线圈的电阻
如图所示，在xoy平面内，第三象限内的直线OM是电场与磁场的边界，OM与负x轴成45°角。在
且OM的左侧空间存在着沿负
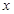方向的匀强电场E，场强大小为32N/C，在
且OM的右侧空间存在着垂直纸面向里的匀强磁场B，磁感应强度大小为0.1T。一不计重力的带负电的粒子，从坐标原点O沿y轴负方向以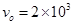
m/s的初速度进入磁场，已知粒子的带电量为
，质量为
，求：
(1)带电粒子第一次经过磁场边界的位置坐标；
(2)带电粒子在磁场区域运动的总时间；(结果保留三位有效数字)
(3)带电粒子最终离开电、磁场区域进入第一象限时的位置坐标。
如图所示，质量为m=1g、电量为q=2´10-6C的带电微粒从偏转极板A、B中间的位置以v0=10m/s的初速度垂直电场方向进入长为L=20cm、距离为d=10cm的偏转电场，出电场后落在距偏转电场x=40cm的挡板上，微粒的落点P离开初速度方向延长线的距离为y2=20cm，不考虑重力的影响。求：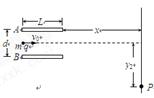
（1）加在A、B两板上的偏转电压UAB；
（2）粒子击中挡板时的动能Ek；
（3）改变偏转电压UAB，则当U¢AB为多少时，微粒落点P¢离开初速度延长线的距离最大？最大距离是多少？
如图所示，电灯L标有“4V1W”字样。滑动变阻器R的总阻值为50Ω，当滑片P滑至某位置时，L恰好正常发光，此时电流表示数为0.45A，由于外电路发生故障，电灯L突然熄灭，此时电流表示数变为0.5A，电压表示数变为10V，若导线完好，电路中各处接触良好，问：
⑴判断电路发生的是什么故障？(无需说明理由)
⑵发生故障前，滑动变阻器接入电路的阻值为多少？
⑶电源的电动势和内电阻分别为多大？
如图，一个粒子电荷量为q=8×10-3C，质量为m＝4×10－6kg，以速度v=2×103m/s穿过磁感强度B＝0.5T、宽度L＝1m的匀强磁场，粒子的重力不计，求：
（1）粒子穿出磁场时，速度方向与初速度方向之间的夹角为多少？
（2）当磁感强度B满足什么条件时，粒子将不能从右侧穿出磁场区域？