某同学利用如图所示的实验装置验证机械能守恒定律.弧形轨道末端水平,离地面的高度为H.将钢球从轨道的不同高度h处静止释放,钢球的落点距轨道末端的水平距离为s.
⑴若轨道完全光滑,s2与h的理论关系应满足s2= (用H、h表示).
⑵该同学经实验测量得到一组数据,如下表所示:
| h(10-1m) |
2.00 |
3.00 |
4.00 |
5.00 |
6.00 |
| s2(10-1m2) |
2.62 |
3.89 |
5.20 |
6.53 |
7.78 |
请在坐标纸上作出s2-h关系图.
⑶对比实验结果与理论计算得到的s2-h关系图线(图中已画出),自同一高度静止释放的钢球,水平抛出的速率 (填“小于”或“大于”)理论值.
⑷从s2-h关系图线中分析得出钢球水平抛出的速率差十分显著,你认为造成上述偏差的可能原因是 .
在学生实验“用DIS研究机械能守恒定律”中,为了研究势能与动能转化时的规律,需要按正确的实验步骤来完成.请按正确的实验顺序填写下列步骤:________.
①开启电源,运行DIS应用软件,点击实验条目中的“研究机械能守恒定律”,软件界面.
②卸下“定位挡片”和“小标尺盘”,安装光电门传感器并接入数据采集器.
③摆锤置于A点,点击“开始记录”,同时释放摆锤,摆锤通过D点的速度将自动记录在表格的对应处.
④把光电门传感器放在大标尺盘最底端约D点,并以此作为零势能点.A、B、C点相对于D点的高度已事先输入,作为计算机的默认值.
⑤点击“数据计算”,计算D点的势能、动能和机械能.
⑥依次将光电门传感器放在标尺盘的C、B点,重复实验,得到相应的数据.在实验过程中,是否有重要的实验步骤遗漏?若有,请写出该步骤的内容:
在学生实验“观察水波的干涉现象”中,下列正确的选项是:
| A.实验器材要选择发波水槽、电动机、电源、电流表等. |
| B.电动机要选择变频电动机. |
| C.实验中要调节两小球击水深度和频率. |
| D.实验中要注意观察两列波叠加区域水面的波形. |
改变实验条件,使两个小球以不同击水,观察不同____的两列波叠加时,水面的波形.
图是研究小车运动时的s-t图的实验装置

①发射器和接收器组成传感器,
②这组传感器测量的物理量是.指出图的s-t图中指定区域内小车的运动状态.
l~2区域:________.
3~4区域:________.
5~6区域:________.
伽利略理想实验将可靠的事实和理论结合起来,能更深刻地反映规律,有关它的实验程序内容如下:
(1)减小第二个斜面的角度,小球在这个斜面上仍能到达原来的高度
(2)两个对接的斜面中,使静止的小球沿一个斜面滚下,小球将滚上另一个斜面。
(3)如果没有摩擦,小球将上升到释放的高度。
(4)继续减小斜面的倾角,最后使它处于水平位置,小球沿水平面做持续的匀速运动。
请按程序先后次序排列,并指出它究竟属于可靠事实,还是通过思维过程的推论,下列选项正确的是()
| A.事实(2)→事实(1)→推论(3)→推论(4) |
| B.事实(2)→推论(1)→推论(3)→推论(4) |
| C.事实(2)→推论(3)→推论(1)→推论(4) |
| D.事实(2)→推论(1)→推论(4)→推论(3) |
做:“互成角度的共点力合成”实验,实验步骤如下: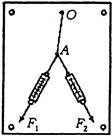
⑴ 在水平放置的木板上,固定一张白纸。
⑵ 把橡皮筋的一端固定在O点,另一端拴两根带套的细线,细线和橡皮筋的交点叫做结点。⑶ 在纸面离O点比橡皮筋略长的距离上标出A点。
⑷ 用两个弹簧秤分别沿水平方向拉两个绳套,把结点拉至A点,如图所示,记下此时两力F1和F2的方向和大小。
⑸ 改用一个弹簧秤沿水平方向拉绳套,仍把结点拉至A点记
下此时力F的方向和大小。
⑹ 撤下弹簧秤和橡皮筋。
⑺ 在A点按同一标度尺,作F1、F2、F力的图示。请你写出下面应继续进行的实验步骤,完成实验。
⑻
⑼