已知椭圆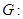
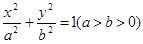 的离心率为
的离心率为 =
= ,椭圆
,椭圆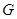 上的点
上的点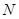 到两焦点的距离之和为12,点A、B分别是椭圆
到两焦点的距离之和为12,点A、B分别是椭圆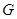 长轴的左、右端点,点F是椭圆的右焦点.点
长轴的左、右端点,点F是椭圆的右焦点.点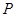 在椭圆上,且位于
在椭圆上,且位于 轴的上方,
轴的上方, .
.
(I) 求椭圆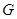 的方程;
的方程;
(II)求点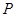 的坐标;
的坐标;
(III) 设 是椭圆长轴AB上的一点,
是椭圆长轴AB上的一点, 到直线AP的距离等于
到直线AP的距离等于 ,求椭圆上的点到点
,求椭圆上的点到点 的距离
的距离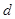 的最小值.
的最小值.
设f(x)=ax3+x恰有三个单调区间,试确定a的取值范围,并求其单调区间.
已知f(x)=x2+c,且f[f(x)]=f(x2+1)
(1)设g(x)=f[f(x)],求g(x)的解析式;
(2)设φ(x)=g(x)-λf(x),试问:是否存在实数λ,使φ(x)在(-∞,-1)内为减函数,且在(-1,0)内是增函数.
设关于x的方程2x2-ax-2=0的两根为α、β(α<β),函数f(x)= .
.
(1)求f(α)·f(β)的值;
(2)证明f(x)是[α,β]上的增函数;
(3)当a为何值时,f(x)在区间[α,β]上的最大值与最小值之差最小?
设x=1与x=2是函数f(x)=alnx+bx2+x的两个极值点.
(1)试确定常数a和b的值;
(2)试判断x=1,x=2是函数f(x)的极大值还是极小值,并说明理由.
在甲、乙两个工厂,甲厂位于一直线河岸的岸边A处,乙厂与甲厂在河的同侧,乙厂位于离河岸40 km的B处,乙厂到河岸的垂足D与A相距50 km,两厂要在此岸边合建一个供水站C,从供水站到甲厂和乙厂的水管费用分别为每千米3a元和5a元,问供水站C建在岸边何处才能使水管费用最省?