如图，△ABC和△ABD都是⊙O的内接三角形，圆心O在边AB上，边AD分别与BC，OC交于E，F两点，点C为
的中点．
（1）求证：OF∥BD；
（2）若
，且⊙O的半径R=6cm．①求证：点F为线段OC的中点； ②求图中阴影部分（弓形）的面积．
已知：如图，在直角坐标系xoy中，点A（2，0），点B在第一象限且△OAB为正三角形，△OAB的外接圆交y轴的正半轴于点C，过点C的圆的切线交x轴于点D．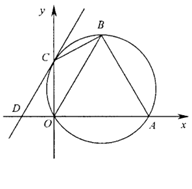
（1）求B、C两点的坐标；
（2）求直线CD的函数解析式；
（3）设E、F分别是线段AB、AD上的两个动点，且EF平分四边形ABCD的周长．
试探究：当点E运动到什么位置时，△AEF的面积最大？最大面积是多少？
已知：关于x的一元一次方程kx=x+2 ①的根为正实数，二次函数y=ax2−bx+kc（c≠0）的图象与x轴一个交点的横坐标为1．（1）若方程①的根为正整数，求整数k的值；
（2）求代数式
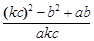的值；（3）求证：关于x的一元二次方程ax2−bx+c="0" ②必有两个不相等的实数根．
．已知如图，正方形AEDG的两个顶点A、D都在⊙O上，AB为⊙O直径，射线线ED与⊙O的另一个交点为C，试判断线段AC与线段BC的关系．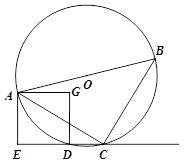
．用尺规作图找出该残片所在圆的圆心O的位置．
（保留作图痕迹，不写作法）
．某体育品商店在销售中发现：某种体育器材平均每天可售出20件，每件可获利40元；若售价减少1元，平均每天就可多售出2件；若想平均每天销售这种器材盈利1200元，那么每件器材应降价多少元？若想获利最大，应降价多少？