某学校抽查了某班级某月10天的用电量,数据如下表(单位:度):
| 度数 |
8 |
9 |
10 |
13 |
14 |
15 |
| 天数 |
1 |
1 |
2 |
3 |
1 |
2 |
(1)这10天用电量的众数是 ,中位数是 ,极差是 ;
(2)求这个班级平均每天的用电量;
(3)已知该校共有20个班级,该月共计30天,试估计该校该月总的用电量.
小明参加某网店的“翻牌抽奖”活动,如图,4张牌分别对应价值5,10,15,20(单位:元)的4件奖品.
(1)如果随机翻1张牌,那么抽中20元奖品的概率为;
(2)如果随机翻2张牌,且第一次翻过的牌不再参加下次翻牌,则所获奖品总值不低于30元的概率为多少?
(1)解方程: ;
;
(2)解不等式组: .
.
计算:(1) ;
;
(2) .
.
如图,抛物线y=ax2+bx﹣ 经过点A(1,0)和点B(5,0),与y轴交于点C.
经过点A(1,0)和点B(5,0),与y轴交于点C.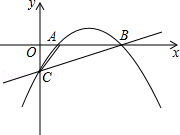
(1)求此抛物线的解析式;
(2)以点A为圆心,作与直线BC相切的⊙A,求⊙A的半径;
(3)在直线BC上方的抛物线上任取一点P,连接PB,PC,请问:△PBC的面积是否存在最大值?若存在,求出这个最大值的此时点P的坐标;若不存在,请说明理由.
如图,P为正方形ABCD的边BC上一动点(P与B、C不重合),连接AP,过点B作BQ⊥AP交CD于点Q,将△BQC沿BQ所在的直线对折得到△BQC′,延长QC′交BA的延长线于点M.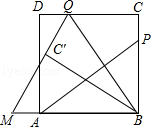
(1)试探究AP与BQ的数量关系,并证明你的结论;
(2)当AB=3,BP=2PC,求QM的长;
(3)当BP=m,PC=n时,求AM的长.