如图,二次函数y=x2+bx+c的图象与x轴交于A、B两点,且A点坐标为
(-3,0),经过B点的直线交抛物线于点D(-2,-3).
(1)求抛物线的解析式和直线BD解析式;
(2)过x轴上点E(a,0)(E点在B点的右侧)作直线EF∥BD,交抛物线于点F,是否存在实数a使四边形BDFE是平行四边形?如果存在,求出满足条件的a;如果不存在,请说明理由.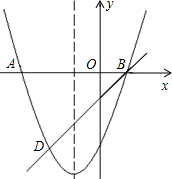
已知:如图,在平面直角坐标系中,O为坐标原点,△OAB的顶点A、B的坐标分别是A(0,5),B(3,1),过点B画BC⊥AB交直线y=﹣m(m> )于点C,连结AC,以点A为圆心,AC为半径画弧交x轴负半轴于点D,连结AD、CD.
)于点C,连结AC,以点A为圆心,AC为半径画弧交x轴负半轴于点D,连结AD、CD.
(1)求证:△ABC≌△AOD;
(2)设△ACD的面积为S,求S关于m的函数关系式;
(3)若四边形ABCD恰有一组对边平行,求m的值.
【提出问题】如图1,小东将一张AD为12,宽AB为4的长方形纸片按如下方式进行折叠:在纸片的一边BC上分别取点P、Q,使得BP=CQ,连结AP、DQ,将△ABP、△DCQ分别沿AP、DQ折叠得△APM,△DQN,连结MN.小东发现线段MN的位置和长度随着点P、Q的位置发生改变.
【规律探索】
(1)请在图1中过点M,N分别画ME⊥BC于点E,NF⊥BC于点F.
求证:①ME=NF;②MN∥BC.
【解决问题】
(2)如图1,若BP=3,求线段MN的长;
(3)如图2,当点P与点Q重合时,求MN的长.
某公司推销一种产品,公司付给推销员的月报酬有两种方案如图所示:其中方案一所示图形是顶点B在原点的抛物线的一部分,方案二所示图形是射线.设推销员推销产品的数量为x(件),付给推销员的月报酬为y(元).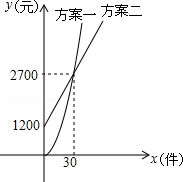
(1)分别求两种方案中y关于x的函数关系式;
(2)当销售达到多少件时,两种方案月报酬差额将达到3800元?
(3)若公司决定改进“方案二”:保持基本工资不变,每件报酬增加m元,使得当销售员销售产量达到40件时,两种方案的报酬差额不超过1000元.求m的取值范围.
如图1是一种包装盒的表面展开图,将它围起来可得到一个几何体的模型.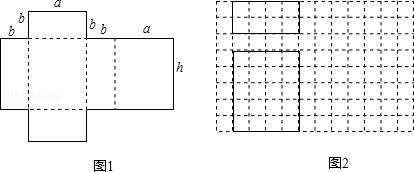
(1)这个几何体模型的名称是 .
(2)如图2是根据a,b,h的取值画出的几何体的主视图和俯视图(图中实线表示的长方形),请在网格中画出该几何体的左视图.
(3)若h=a+b,且a,b满足 a2+b2﹣a﹣6b+10=0,求该几何体的表面积.
a2+b2﹣a﹣6b+10=0,求该几何体的表面积.
如图是由梯子A B和梯子AC搭成的脚手架,其中AB=AC=5米,∠α=70°.
(1)求梯子顶端A离地面的高度AD的长和两梯脚之间的距离BC的长.
(2)生活经验告诉我们,增大两梯脚之间的距离可降低梯子的高度,若BC长达到6米,则梯子的高度下降多少米?(以上结果均精确到0.1米,供参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)