一工地计划租用甲、乙两辆车清理淤泥，从运输量来估算：若租两车合运，10天可以完成任务；若单独租用乙车完成任务则比单独租用甲车完成任务多用15天.
（1）甲、乙两车单独完成任务分别需要多少天？
（2）已知两车合运共需租金65000元，甲车每天的租金比乙车每天的租金多1500元，试问：租甲乙两车、单独租甲车、单独租乙车这三种租车方案中，哪一种租金最少？请说明理由.
已知AB∥DE，∠B=60°，且CM平分∠DCB，CM⊥CN，垂足为C，求∠NCE的度数．
某校对学生是否自导母亲生日情况进行抽样调查，调查结果绘制成的如下的扇形统计图和条形统计图，根据图示信息，解答下列问题：
（1）求本次被调查学生的人数，并补全条形统计图；
（2）若全校共有2700名学生，请你估计该校有多少名学生知道母亲的生日？
已知△ABC各顶点的坐标为A（﹣4，﹣2），B（﹣1，﹣3），C（﹣2，﹣1），将△ABC先向右平移4个单位长度，再向上平移3个单位长度得到△A′B′C′．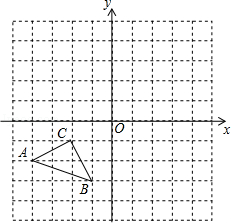
（1）在直角坐标系中画出△A′B′C′；
（2）求出△A′B′C′的面积．
解不等式组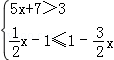
，并将解集在数轴上表示出来．
（1）计算：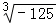
﹣
+|﹣
|﹣
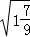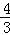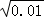
（2）解方程组
．