(本题满分13分)
已知直线 与椭圆
与椭圆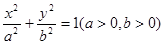 相交于A、B两点.
相交于A、B两点.
(Ⅰ)若椭圆的离心率为 ,焦距为2,求线段AB的长;
,焦距为2,求线段AB的长;
(Ⅱ)若向量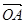 与向量
与向量 互相垂直(其中O为坐标原点),当椭圆的离心率
互相垂直(其中O为坐标原点),当椭圆的离心率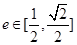 时,求椭圆的长轴长的最大值.
时,求椭圆的长轴长的最大值.
某小卖部为了了解热茶销售量与气温之间的关系,随机统机并制作了某6天卖出的热茶的杯数与当天气温的对比表:
| 气温(℃) |
26 |
18 |
13 |
10 |
4 |
 |
| 杯数 |
20 |
24 |
34 |
38 |
50 |
64 |
画出散点图并判断热茶销售量与气温之间是否具有线性相关关系
我们知道:圆的任意一弦(非直径)的中点和圆心的连线与该弦垂直;那么,若椭圆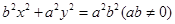 的一弦(非过原点的弦)中点与原点的连线及弦所在直线的斜率均存在,你能得到什么结论?请予以证明.
的一弦(非过原点的弦)中点与原点的连线及弦所在直线的斜率均存在,你能得到什么结论?请予以证明.
一个平面用n条直线去划分,最多将平面分成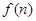 个部分.
个部分.
(1)求 ;
;
(2)观察 ,
, ,
, 有何规律;
有何规律;
(3)求出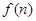
已知数列 中,
中, ,
, ,
,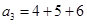 ,
, 请归纳
请归纳 等于多少?并说明理由
等于多少?并说明理由
用三段论证明:直角三角形两锐角之和为90°